返回

初中一年级数学

首页
首页 初中一年级数学知识 对顶角，同位角，内错角，同旁内角 平行线的判定 垂直的判定与性质 试题正文
  • 填空题
    有以下四个命题：①经过直线外一点，有且只有一条直线与已知直线平行；②经过直线外或直线上一点，有且只有一条直线与已知直线垂直；③两直线被第三条直线所截，同旁内角互补；④两平行直线被第三条直线所截，内错角相等．那么，其中正确命题的序号是（    ）．  （把你认为正确的命题序号都填上）
    本题信息：2011年浙江省期末题数学填空题难度一般 来源:丁慧芳（初中数学）
  • 本题答案
    查看答案
本试题 “有以下四个命题：①经过直线外一点，有且只有一条直线与已知直线平行；②经过直线外或直线上一点，有且只有一条直线与已知直线垂直；③两直线被第三条直线所截，...” 主要考查您对

对顶角，同位角，内错角，同旁内角

平行线的判定

垂直的判定与性质

等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
  • 对顶角，同位角，内错角，同旁内角
  • 平行线的判定
  • 垂直的判定与性质

对顶角：
一个角的两边分别是另一个角的反向延升线，这两个角是对顶角两条直线相交后所得的只有一个公共顶点且两个角的两边互为反向延长线，这样的两个角叫做互为对顶角。
两条直线相交，构成两对对顶角。互为对顶角的两个角相等（对顶角的性质）。
对顶角是针对具有特殊位置的两个角的名称；
对顶角相等反映的是两个角之间的大小关系。

同位角：两个都在截线的同旁，又分别处在被截的两条直线同侧的位置的角叫做同位角。

内错角：两个角分别在截线的两侧，且在两条被截直线之间，具有这样位置关系的一对角叫做内错角。

同旁内角： 两个角都在截线的同一侧，且在两条被截线之间，具有这样位置关系的一对角互为同旁内角。


各种角的关系图示：

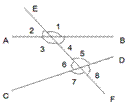
直线AB，CD与EF相交（或者说两条直线AB，CD被第三条直线EF所截），构成八个角。
如图中，∠1与∠3，∠2与∠4是对顶角。
其中∠1与∠5这两个角分别在AB，CD的上方，并且在EF的同侧，像这样位置相同的一对角叫做同位角；
∠3与∠5这两个角都在AB，CD之间，并且在EF的异侧，像这样位置的两个角叫做内错角；
∠3与∠6在直线AB，CD之间，并侧在EF的同侧，像这样位置的两个角叫做同旁内角。
平行线的概念：
在同一个平面内，不相交的两条直线叫做平行线。平行用符号“∥，如“AB∥CD”，读作“AB平行于CD”。
注意：
①平行线是无限延伸的，无论怎样延伸也不相交。
②当遇到线段、射线平行时，指的是线段、射线所在的直线平行。

平行线的判定平行线的判定公理：
（1）两条直线被第三条直线所截，如果同位角相等，那么两直线平行。简称：同位角相等，两直线平行。
（2）两条直线被第三条直线所截，如果内错角相等，那么两直线平行。简称：内错角相等，两直线平行。
（3）两条直线被第三条直线所截，如果同旁内角互补，那么两直线平行。简称：同旁内角互补，两直线平行。
还有下面的判定方法：
（1）平行于同一条直线的两直线平行。
（2）垂直于同一条直线的两直线平行。
（3）平行线的定义。

判定方法的逆应用：
在同一平面内，两直线不相交，即平行。
两条直线平行于一条直线，则三条不重合的直线互相平行。
两直线平行，同位角相等。
两直线平行，内错角相等。
两直线平行，同旁内角互补。
6a⊥c，b⊥c则a∥b。


垂线的定义：
两条直线相交所成的四个角中，有一个角是直角时，就说这两条直线互相垂直。其中一条直线叫做另一条直线的垂线，它们的交点叫做垂足。
直线AB，CD互相垂直，记作“AB⊥CD”（或“CD⊥AB”)，读作“AB垂直于CD”（或“CD垂直于AB”）。
垂线的性质：
性质1：过一点有且只有一条直线与已知直线垂直。
性质2：连结直线外一点与直线上各点的所有线段中，垂线段最短。简称：垂线段最短。
垂直的判定：垂线的定义。
发现相似题
与“有以下四个命题：①经过直线外一点，有且只有一条直线与已知直...”考查相似的试题有：