本试题 “已知向量a=(cos32x,sin32x),b=(cosx2,-sinx2),且x∈[π2,32π](1)求|a+b|的取值范围;(2)求函数f(x)=a•b-|a+b|的最小值,并求此时x的值.” 主要考查您对已知三角函数值求角
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 已知三角函数值求角
反三角函数的定义:
(1)反正弦:在闭区间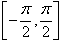 上符合条件sinx=a(-1≤a≤1)的角x,叫做实数a的反正弦,记作arcsina,即x=arcsina,其中x∈
上符合条件sinx=a(-1≤a≤1)的角x,叫做实数a的反正弦,记作arcsina,即x=arcsina,其中x∈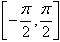 ,且a=sinx;
,且a=sinx;
注意arcsina表示一个角,这个角的正弦值为a,且这个角在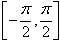 内(-1≤a≤1)。
内(-1≤a≤1)。
(2)反余弦:在闭区间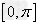 上,符合条件cosx=a(-1≤a≤1)的角x,叫做实数a的反余弦,记作arccosa,即x=arccosa,其中x∈[0,π],且a=cosx。
上,符合条件cosx=a(-1≤a≤1)的角x,叫做实数a的反余弦,记作arccosa,即x=arccosa,其中x∈[0,π],且a=cosx。
(3)反正切:在开区间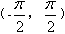 内,符合条件tanx=a(a为实数)的角x,叫做实数a的反正切,记做arctana,即x=arctana,其中x∈
内,符合条件tanx=a(a为实数)的角x,叫做实数a的反正切,记做arctana,即x=arctana,其中x∈ ,且a=tanx。
,且a=tanx。
反三角函数的性质:
(1)sin(arcsina)=a(-1≤a≤1),cos(arccosa)=a(-1≤a≤1),
tan(arctana)=a;
(2)arcsin(-a)=-arcsina,arccos(-a)=π-arccosa,arctan(-a)=-arctana;
(3)arcsina+arccosa=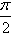 ;
;
(4)arcsin(sinx)=x,只有当x在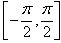 内成立;同理arccos(cosx)=x只有当x在闭区间[0,π]上成立。
内成立;同理arccos(cosx)=x只有当x在闭区间[0,π]上成立。
已知三角函数值求角的步骤:
(1)由已知三角函数值的符号确定角的终边所在的象限(或终边在哪条坐标轴上);
(2)若函数值为正数,先求出对应锐角α1,若函数值为负数,先求出与其绝对值对应的锐角α1;
(3)根据角所在象限,由诱导公式得出0~2π间的角,如果适合条件的角在第二象限,则它是π-α1;如果适合条件的角在第三象限,则它是π+α1;在第四象限,则它是2π-α1;如果是-2π到0的角,在第四象限时为-α1,在第三象限为-π+α1,在第二象限为-π-α1;
(4)如果要求适合条件的所有角,则利用终边相同的角的表达式来写出。
与“已知向量a=(cos32x,sin32x),b=(cosx2,-sinx2),且x∈[π2,3...”考查相似的试题有:
- 已知f(x)=sin2x-cos2x+11+ctgx①化简f(x);②若sin(x+π4)=35,且π4<x<34π,求f(x)的值.
- 已知a=(sinx,sinx),b=(cosx,sinx),记f(x)=a•b求(1)f(π3)的值;(2)函数f(x)的最小值及相应的x值.
- 在△ABC中,sinB•sinC=cos2A2,则△ABC的形状是______.
- 在△ABC中,a、b、c分别是三内角A、B、C所对边的长,若bsinA=asinC,则△ABC的形状( )A.钝角三角形B.直角三角形C.等腰三角...
- 已知,且,则α=( )。
- 设集合P={x|sinx=1,x∈R},Q={x|cosx=-1,x∈R},则( )A.P∩Q=∅B.P⊆QC.P∪Q={x|x=kπ2,k∈Z}D.P=Q
- 已知a=(1,cosx),b=(13,sinx),x∈(0,π)(1)若a∥b,求sinx+cosxsinx-cosx的值;(2)若a⊥b,求sinx-cosx的值.
- cosπ17cos2π17cos4π17cos8π17=______.
- 函数f(x)=sin2x+cos2x-12的最小正周期是______.
- 已知函数f(x)=a(2cos2x2+sinx)+b.(Ⅰ)当a=1时,求函数f(x)的单调递增区间;.(Ⅱ)当a<0时,若x∈[0,π],函数f(x)的值...