本试题 “聪明的小法官。(对的打“√”,错的打“×”)(1)方程是等式,等式包括方程。[ ](2)面积相等的三角形,形状一定相等。[ ](3)当长方形和平行四边形的周长相等...” 主要考查您对长方形的面积
求小数的近似值
三角形的面积
小数乘法
方程的定义,等式的性质
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 长方形的面积
- 求小数的近似值
- 三角形的面积
- 小数乘法
- 方程的定义,等式的性质
学习目标:
理解掌握长方形面积计算公式,并且会运用公式进行计算。
面积公式:
长方形面积=长×宽,用字母表示:S=ab。
理解掌握长方形面积计算公式,并且会运用公式进行计算。
面积公式:
长方形面积=长×宽,用字母表示:S=ab。
求近似数:
是根据需要用“四舍五入法”保留一定的小数位数。
方法点拨:
求近似数时:保留整数,表示精确到个位;保留一位小数,表示精确到十分位;保留两位小数,表示精确到百分位……
如:豆豆身高0.984米
求:1、保留两位小数:
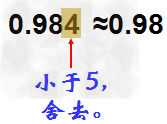
如果保留两位小数,就要第三位数省略。
2、保留一位小数:

如果保留一位小数,就要把第二、三位小数省略。
在表示近似数时,小数末尾的0不能去掉。
3、保留整数部分:
 ≈1
≈1
省略个位后面的尾数
是根据需要用“四舍五入法”保留一定的小数位数。
方法点拨:
求近似数时:保留整数,表示精确到个位;保留一位小数,表示精确到十分位;保留两位小数,表示精确到百分位……
如:豆豆身高0.984米
求:1、保留两位小数:

如果保留两位小数,就要第三位数省略。
2、保留一位小数:

如果保留一位小数,就要把第二、三位小数省略。
在表示近似数时,小数末尾的0不能去掉。
3、保留整数部分:
 ≈1
≈1省略个位后面的尾数
学习目标:
1、理解三角形面积公式
2、会根据公式进行面积计算
图形拼组:
1、两个完全一样的锐角三角形,可以拼成一个平行四边形。
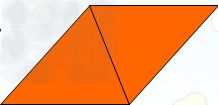
2、两个完全一样的钝角三角形,可以拼成一个平行四边形。
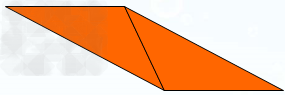
面积公式:
三角形面积=底×高÷2,用字母表示:S=ah÷2。
1、理解三角形面积公式
2、会根据公式进行面积计算
图形拼组:
1、两个完全一样的锐角三角形,可以拼成一个平行四边形。

2、两个完全一样的钝角三角形,可以拼成一个平行四边形。

面积公式:
三角形面积=底×高÷2,用字母表示:S=ah÷2。
学习目标:
理解小数乘以整数的计算方法及算理。
方法点拨:
按照整数乘法法则先求出积,看因数中一共有几位小数,就从积的右边数几位点上小数点。
小数乘整数:一个数乘以小数就是求这个数的几分之几、百分之几……是多少;
小数乘小数:在给积点小数点时,乘得的积的小数位数不够时,要在前面用0补足。
理解小数乘以整数的计算方法及算理。
方法点拨:
按照整数乘法法则先求出积,看因数中一共有几位小数,就从积的右边数几位点上小数点。
小数乘整数:一个数乘以小数就是求这个数的几分之几、百分之几……是多少;
小数乘小数:在给积点小数点时,乘得的积的小数位数不够时,要在前面用0补足。
等式:
含有等号的式子叫做等式(数学术语)。形式:把相等的两个数(或字母表示的数)用“=”连接起来。
方程:
含有未知数的等式叫做方程。即:
1.方程中一定有一个或一个以上含有未知数的代数式;
2.方程式是等式,但等式不一定是方程。
含有等号的式子叫做等式(数学术语)。形式:把相等的两个数(或字母表示的数)用“=”连接起来。
方程:
含有未知数的等式叫做方程。即:
1.方程中一定有一个或一个以上含有未知数的代数式;
2.方程式是等式,但等式不一定是方程。
等式基本性质:
性质1
等式两边同时加上(或减去)同一个整式,等式的值不变。
若a=b
那么a+c=b+c
性质2
等式两边同时乘或除以同一个不为0的整式,等式的值不变。
若a=b
那么有a·c=b·c
或a÷c=b÷c (c≠0)
性质3
等式具有传递性。
若a1=a2,a2=a3,a3=a4,……an=an,那么a1=a2=a3=a4=……=an
发现相似题
与“聪明的小法官。(对的打“√”,错的打“×”)(1)方程是等式,等...”考查相似的试题有:
- 花园有一个正方形的草坪,它的周长是在20厘米,面积是多少平方厘米?(1)画出平面图.(2)算出占地面积?
- 8.09666保留一位小数是______,保留两位小数是______.
- 如图,AB=5BE,BC=4CF,AC=3CD,求三角形DEF和三角形ABC面积的比.
- 一个平行四边形的底是40厘米,高是20厘米,与它等底等高的三角形的面积是( )A.4平方分米B.400平方分米C.8平方分米
- 直接写得数.0.8×25=0×4.32=0.57+0.43=4.87-1.7=0.02×500=2.8×10=3.6+0.4=2.4×0.2=1.05×8=0.04×1.5=0.42-0.37=3.64+2.36=
- 3.49×2.8的积保留两位小数约______.
- 3个2.2是多少?
- a、b是两个不为零的数,若a的12等b的13,那么b是a的23.______.(判断对错)
- 等式不一定是方程,方程一定是等式.______.
- 下面式子中,不是方程的是[ ]A.x=5B.0.1x=5C.5x=0.1D.5x