本试题 “仔细推敲,认真辨析。(对的打“√”,错的打“×”)(1)每个公民一出生,就有一个身份证号码,共18位数,其中倒数第二位的数字是用来表示性别的。 [ ](2)把19...” 主要考查您对有余数的除法
数字和编码
抽屉原理
合理安排时间
可能性,概率
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 有余数的除法
- 数字和编码
- 抽屉原理
- 合理安排时间
- 可能性,概率
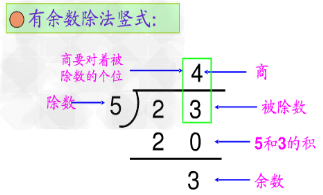
思路点拨:
1、有余数的除法中,余数比除数小。
2、被除数÷除数=商……余数
被除数=商×除数+余数
除数=(被除数-余数)÷商
商=(被除数-余数)÷除数
数字和编码在实际生活中的应用主要表现在:
身份证中的数字,电话,邮政编码,车牌号,食品袋上的磁条等等都有不同的含义。
身份证号码的编码含义:
数字编码实际应用于很多领域,比如:身份证号码、学号、车牌号、邮政编码、电话区号、银行帐号等等。
身份证号码共18位:AAAAAABBBBBBCCCD
1、号码的结构
公民身份号码是特征组合码,由十七位数字本体码和一位校验码组成。排列顺序从左至右依次为:六位数字地址码,八位数字出生日期码,三位数字顺序码和一位数字校验码。
2、地址码(前六位数)
表示编码对象常住户口所在县(市、旗、区)的行政区划代码,按GB/T2260的规定执行。
3、出生日期码(第七位至十四位)
表示编码对象出生的年、月、日,按GB/T7408的规定执行,年、月、日代码之间不用分隔符。
4、顺序码(第十五位至十七位)
表示在同一地址码所标识的区域范围内,对同年、同月、同日出生的人编定的顺序号,顺序码的奇数分配给男性,偶数分配给女性。
5、校验码(第十八位数)
作为尾号的校验码,是由号码编制单位按统一的公式计算出来的,如果某人的尾号是0-9,都不会出现X,但如果尾号是10,那么就得用X来代替,因为如果用10做尾号,那么此人的身份证就变成了19位。X是罗马数字的10,用X来代替10,可以保证公民的身份证符合国家标准。
又称鸽巢原理,它是组合数学的一个基本原理,最先是由德国数学家狭利克雷明确地提出来的,因此,也称为狭利克雷原理。
在这类问题中,只需要确定某个物体(或某个人)的存在就可以了,并不需要指出是哪个物体(或哪个人),也不需要说明是通过什么方式把这个存在的物体(或人)找出来。这类问题依据的理论,我们称之为“抽屉原理”。
两种抽屉原理:
第一抽屉原理:
原理1: 把多于n个的物体放到n个抽屉里,则至少有一个抽屉里的东西不少于两件。
原理2 :把多于mn(m乘以n)个的物体放到n个抽屉里,则至少有一个抽屉里有不少于m+1的物体。
原理3 :把无穷多件物体放入n个抽屉,则至少有一个抽屉里 有无穷个物体。
原理1 、2 、3都是第一抽屉原理的表述。
第二抽屉原理:
把(mn-1)个物体放入n个抽屉中,其中必有一个抽屉中至多有(m—1)个物体(例如,将3×5-1=14个物体放入5个抽屉中,则必定有一个抽屉中的物体数少于等于3-1=2)。
抽屉原理形式:
形式一:把m个物体任意分放进n个空抽屉里(m>n,n是非0自然数),那么一定有一个抽屉中放进了至少2个物体。
形式二:把多于kn个物体任意分放进n个空抽屉里(k是正整数),那么一定有一个抽屉中放进了至少(k+1)个物体。
作息时间规划的五个步骤:
第一步,列出每日必须进行的各项活动。比如上课、写作业、睡眠、吃饭、上下学、体育锻炼、看新闻联播……
第二步,根据自己现在的生活习惯,安排好各项活动的基本顺序。如起床、洗漱、早餐、上学、上课……
第三步,测算各项活动的时间长度。你可以观察和记录自己近期做每一件事情所花费的平均时间作为参考。
第四步,根据劳逸结合、科学用脑,以及交叉安排、高效学习的原则调整各项活动的顺序和学习时间安排。
最基本的思路是:
a两项学习活动之间应该安排生活、劳动等其他活动;
b学习时间比较长(90分钟以上)时应该安排两门课程(最好是文理科)间插复习或者两种方式(阅读和解题)间插学习。
第五步,根据效果调整作息时间表。每个适合自身情况的作息时间表都不是一次形成的,我们需要根据每日作息时间表的执行情况调整各个项目的顺序或者是时间长度的安排,直到找到一个符合自身情况的作息时间表为止。
合理安排时间的名言:
合理安排时间,就等于节约时间。--培根
利用时间是一个极其高级的规律。 ---恩格斯
今天应做的事没有做,明天再早也是耽误了。---裴斯泰洛齐
人生有一道难题,那就是如何使一寸光阴等于一寸生命
庸人费心将是消磨时光,能人费尽心计利用时间
抓住今天,尽可能少的信赖明天
时间是我的财产,我的田亩是时间。——歌德
完成工作的方法是爱惜每一分钟。 --达尔文
可能性:
是指事物发生的概率,是包含在事物之中并预示着事物发展趋势的量化指标。有些事件的发生是确定的,有些是不确定的。用“可能”、“不可能”“一定”等表达事物发生的情况。
常见方法有:抛骰子、摸球、转盘。
概率:
又称或然率、机会率或机率、可能性,是数学概率论的基本概念,是一个在0到1之间的实数,是对随机事件发生的可能性的度量。
随机事件:
有些事件在一定的条件下可能发生,也可能不发生,结果不确定。例如,购买彩票能否 中奖,开出的列车能否正点到达。明年今天是否下雨等待,我们称之为随机事件。
我们用随机事件的“概率”来表示随机事件发生可能性大小:概率是0到1之间的一个数,概率随机事件发生的可能性大。
在小学阶段我们只计算最简单的一些随机事件的概率,这种计算方法以“等可能性”为基础。在有些情况下,虽然有些事情的结果是不确定的(随机性的),但是由于某种“对称性”,不同的基本结果发生的可能性是相同的,这时,我们说这些基本结果是等可能的,从而确定相关事件的概率。例如:
投一枚均匀硬币,“出现正面”“出现反面”这两种基本结果是等可能的,所以“出现正面”和“出现反面”的概率都是1/2;
投一枚色子(骰子),“出现1点”“出现2点”......“出现6点”这六种基本情况是等可能的,其概率是1/6 。
对于随机事件,我们关心的是事件发生的可能性。
事件发生的可能性大小是可以比较的,所以人们常说一件事情“不可能”""不大可能”“很可能”“非常可能”“绝对可能”......这些说法反应可能性大小的不同程度。
射击时,“射中十环”的可能性比“射中九环”的可能性小;
一分钟投篮,“投中15个”比“投中10个”的可能性小
与“仔细推敲,认真辨析。(对的打“√”,错的打“×”)(1)每个公民...”考查相似的试题有:
- ______÷5=14…______.
- 19÷6=( )……( )
- ◇◇÷□=12…1,□内共有( )种填法.A.8种B.9种C.7种
- 除数是一位数的除法,余数最大是8______.
- 看图列式计算。(1)列式: (2)28枝列式:
- 猴山上6只猴分桃,总有1只猴至少分到了5个桃。这堆桃至少有多少个呢?
- 一个布袋里有10个黑扣子,任意摸一个,一定是( ),( )是白扣子。
- 盒子里有9个红色跳棋,2个黄色跳棋。任意摸出一个,可能出现( )种情况,分别是( )和( ),摸出( )色跳棋的可能性大。
- 太阳从西方升起是( )发生的事情。
- 小明转转盘.转盘的箭头每被旋转一次,猜一猜:指向红色区域的可能性是()(),指向黄色区域的可能性是()(),指向白色区域的可...