本试题 “已知一个底面为菱形的直棱柱,高为10cm,体积为150cm3,则这个棱柱的下底面积为( )cm2;若该棱柱侧面展开图的面积为200cm2,记底面菱形的顶点依次为A,B,C...” 主要考查您对认识立体几何图形
几何体的展开图
菱形,菱形的性质,菱形的判定
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 认识立体几何图形
- 几何体的展开图
- 菱形,菱形的性质,菱形的判定
立体几何图形:
从实物中抽象出来的各种图形,统称为几何图形,几何图形是数学研究的主要对象之一。有些几何图形(如长方体、正方体、圆柱、圆锥、球等)的各个部分不都在同一平面内,它们是立体图形。由一个或多个面围成的可以存在于现实生活中的三维图形。点动成线,线动成面,面动成体。即由面围成体,看一个体最多看到立体图形实物三个面。
常见立体几何图形及性质:
①正方体:
有8个顶点,6个面。每个面面积相等(或每个面都有正方形组成)。有12条棱,每条棱长的长度都相等。(正方体是特殊的长方体)
②长方体:
有8个顶点,6个面。每个面都由长方形或相对的一组正方形组成。有12条棱,相对的4条棱的棱长相等。
③圆柱:
上下两个面为大小相同的圆形。有一个曲面叫侧面。展开后为长方形或正方形或平行四边形。有无数条高,这些高的长度都相等。
④圆锥:
有1个顶点,1个曲面,一个底面。展开后为扇形。只有1条高。四面体有1个顶点,四面六条棱高。
⑤直三棱柱:
三条侧棱切平行,上表面和下表面是平行且全等的三角形。
⑥球:
球是生活中最常见的图形之一,例如篮球、足球都是球,球是由一个面所围成的几何体。
常见的立体几何图形视图:
从实物中抽象出来的各种图形,统称为几何图形,几何图形是数学研究的主要对象之一。有些几何图形(如长方体、正方体、圆柱、圆锥、球等)的各个部分不都在同一平面内,它们是立体图形。由一个或多个面围成的可以存在于现实生活中的三维图形。点动成线,线动成面,面动成体。即由面围成体,看一个体最多看到立体图形实物三个面。
常见立体几何图形及性质:
①正方体:
有8个顶点,6个面。每个面面积相等(或每个面都有正方形组成)。有12条棱,每条棱长的长度都相等。(正方体是特殊的长方体)
②长方体:
有8个顶点,6个面。每个面都由长方形或相对的一组正方形组成。有12条棱,相对的4条棱的棱长相等。
③圆柱:
上下两个面为大小相同的圆形。有一个曲面叫侧面。展开后为长方形或正方形或平行四边形。有无数条高,这些高的长度都相等。
④圆锥:
有1个顶点,1个曲面,一个底面。展开后为扇形。只有1条高。四面体有1个顶点,四面六条棱高。
⑤直三棱柱:
三条侧棱切平行,上表面和下表面是平行且全等的三角形。
⑥球:
球是生活中最常见的图形之一,例如篮球、足球都是球,球是由一个面所围成的几何体。
常见的立体几何图形视图:
| 几何图形 | 图形 |
| 长方体 |  |
| 正方体 |  |
| 圆锥 |  |
| 圆柱 |  |
| 圆锥 | 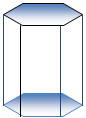 |
| 球 |  |
有些立体图形是由一些平面图形围成的,将它们的表面适当的剪开,可以展开成平面图形,这样的平面图形称为相应立体图形的展开图。
几何体展开图规律:
1.沿多面体的棱将多面体剪开成平面图形,若干个平面图形也可以围成一个多面体;
2.同一个多面体沿不同的棱剪开,得到的平面展开图是不一样的,就是说:同一个立体图形可以有多种不同的展开图。
注意:
①正方体展开头记忆口诀:
正方体盒巧展开,六个面儿七刀裁;
十四条边布周围,十一类图记分明;
四方成线两相卫,六种图形巧组合;
跃马失蹄四分开;两两错开一阶梯。
对面相隔不相连,识图巧排“7”、“凹”、“田”。
②在正方体的展开图中,一条直线上的小正方形不会超过四个。
③正方体的展开图不会有"田"字形,"凹"字形的形状。
图形展开图:
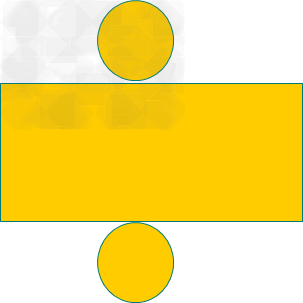
1.圆柱展开图:
 →→
→→
2.圆锥展开图:
 →→
→→
3.长方体展开图:
 →→
→→
4.正方体展开图:
 →→
→→
5.三棱柱展开图:
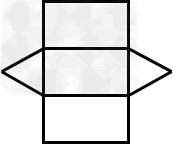
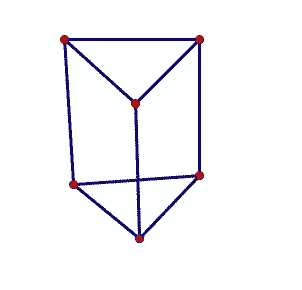 →→
→→
6.三棱锥展开图:
 →→
→→
菱形的定义:
在一个平面内,有一组邻边相等的平行四边形是菱形。
在一个平面内,有一组邻边相等的平行四边形是菱形。
菱形的性质:
①菱形具有平行四边形的一切性质;
②菱形的对角线互相垂直且平分,并且每一条对角线平分一组对角;
③菱形的四条边都相等;
④菱形既是轴对称图形(两条对称轴分别是其两条对角线所在的直线),也是中心对称图形(对称中心是其重心,即两对角线的交点);
⑤在有一个角是60°角的菱形中,较短的对角线等于边长,较长的对角线是较短的对角线的根号3倍。
菱形的判定:
在同一平面内,
(1)定义:有一组邻边相等的平行四边形是菱形
(2)定理1:四边都相等的四边形是菱形
(3)定理2:对角线互相垂直的平行四边形是菱形
菱形是在平行四边形的前提下定义的,首先它是平行四边形,而且是特殊的平行四边形,特殊之处就是“有一组邻边相等”,因而增加了一些特殊的性质和判定方法。
菱形的面积:S菱形=底边长×高=两条对角线乘积的一半。
发现相似题
与“已知一个底面为菱形的直棱柱,高为10cm,体积为150cm3,则这...”考查相似的试题有:
- 如图所示为一个无盖长方体盒子的展开图(重叠部分不计),根据图中数据,可知该无盖长方体的容积为 ( )A.4B.6C.8D.12
- 如图,是一个正方体的平面展开图,原正方体中“祝”的对面是【 】A.考B.试C.顺D.利
- 如图,六个大小一样的小正方形的标号分别是A,B,…,F,它们拼成如图的形状,则三对对面的标号分别是______.
- 如图中的四个图形每个均由六个相同的正方形组成,折叠后能围成正方体的是( )A.B.C.D.
- 下面的图形经过折叠能围成正方体的是[ ]A.B.C.D.
- 如图,在□ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=,则AF的长为__________.
- 菱形四边的中点到______的距离相等,因此菱形各边的中点在以______为圆心,以______为半径的圆上.
- 如图,等腰△OBD中,OD=BD,△OBD绕点O逆时针旋转一定角度后得到△OAC,此时正好B、D、C在同一直线上,且点D是BC的中点.小题1:求...
- 下列给出的条件中,能判定四边形ABCD是平行四边形的为( ).A.AB=BC,AD=CDB.AB=CD,AD∥BCC.∠A=∠B,∠C=∠DD.AB∥CD,∠A=∠C
- 如图11,E、F分别是矩形ABCD的对角线AC和BD上的点,且AE=DF。求证:BE=CF