本试题 “(本小题满分12分)甲乙两名射手互不影响地进行射击训练,根据以往的数据统计,他们设计成绩的分布列如下:射手甲射手乙环数8910环数8910概率概率(Ⅰ)若甲乙...” 主要考查您对离散型随机变量的期望与方差
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 离散型随机变量的期望与方差
数学期望的定义:
称 为ξ的数学期望或平均数,均值,数学期望又简称为期望,它反映了随机变量取值的平均水平。
为ξ的数学期望或平均数,均值,数学期望又简称为期望,它反映了随机变量取值的平均水平。
方差的定义:
称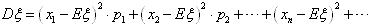 为ξ的均方差,简称为方差,
为ξ的均方差,简称为方差,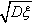 叫做随机变量ξ的标准差,记作:
叫做随机变量ξ的标准差,记作: 。
。
期望与方差的性质:
(1)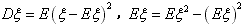 ;
;
(2)若η=aξ+b,则 ;
;
(3)若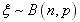 ,则
,则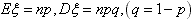 ;
;
(4)若ξ服从几何分布,则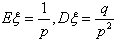 。
。
求均值(数学期望)的一般步骤:
(1)首先判断随机变量是否服从二点分布、二项分布或超几何分布,若服从,则直接用公式求均值.(2)若不服从特殊的分布,则先求出随机变量的分布列,再利用公式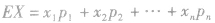 求均值。
求均值。
方差的求法:
(1)若随机变量X服从二点分布或二项分布,则直接利用方差公式可求.
(2)若随机变量X不服从特殊的分布时,求法为:
发现相似题
与“(本小题满分12分)甲乙两名射手互不影响地进行射击训练,根...”考查相似的试题有:
- 已知一个盒子中装有3个黑球和4个白球,现从该盒中摸出3个球,假设每个球被摸到的可能性相同.(Ⅰ)若3个球是逐个摸出的(摸出...
- 同时抛掷4枚质地均匀的硬币80次,设4枚硬币恰好出现2枚正面向上2枚反面向上的次数为X,则X的数学期望是( ) A.20 B.25 C....
- 自主招生是高校在高考前争抢优等生的一项重要举措,不少同学也把自主招生当做高考前的一次锻炼,可谓是一层锻炼一层认识呀....
- 某中学校本课程共开设了A,B,C,D共4门选修课,每个学生必须且只能选修1门课程课,现有该校的甲、乙、丙3名学生:(I)求恰...
- 设ξ~B(n,p)且Eξ=15,Dξ=,则n、p的值分别是A.50,B.60,C.50,D.60,
- (本小题满分12分)东莞市政府要用三辆汽车从新市政府把工作人员接到老市政府,已知从新市政府到老市政府有两条公路,汽车走...
- 签盒中有编号为1、2、3、4、5、6的6支签,从中任意取3支,设X为这3支签的号码之中最大的一个.则X的均值为( ) A.5 B.5.25...
- 为从甲、乙两名运动员中选拔一人参加2010年广州亚运会跳水项目,对甲、乙两名运动员进行培训.现分别从他们在培训期间参加的...
- 某单位对应聘者甲、乙、丙进行面试,并从专业知识、工作经验、仪表形象三方面给应聘者打分,每一方面满分20分,最后的打分情...
- 甲、乙、丙、丁4名同学被随机地分到A、B、C三个社区参加社会实践,要求每个社区至少有一名同学。(Ⅰ)求甲、乙两人都被分到A...