本试题 “如图,点A的坐标为(-1,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为_________。” 主要考查您对正比例函数的定义
正比例函数的图像
一次函数的定义
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 正比例函数的定义
- 正比例函数的图像
- 一次函数的定义
正比例函数定义:
一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数。
正比例函数属于一次函数,但一次函数却不一定是正比例函数。
正比例函数是一次函数的特殊形式,即一次函数y=kx+b中,若b=0,即所谓“y轴上的截距”为零,则为正比例函数。
正比例函数的关系式表示为:y=kx(k为比例系数)
当k>0时(一三象限),k越大,图像与y轴的距离越近。函数值y随着自变量x的增大而增大。
当k<0时(二四象限),k越小,图像与y轴的距离越近。自变量x的值增大时,y的值则逐渐减小。
一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数。
正比例函数属于一次函数,但一次函数却不一定是正比例函数。
正比例函数是一次函数的特殊形式,即一次函数y=kx+b中,若b=0,即所谓“y轴上的截距”为零,则为正比例函数。
正比例函数的关系式表示为:y=kx(k为比例系数)
当k>0时(一三象限),k越大,图像与y轴的距离越近。函数值y随着自变量x的增大而增大。
当k<0时(二四象限),k越小,图像与y轴的距离越近。自变量x的值增大时,y的值则逐渐减小。
正比例函数性质:
定义域
R(实数集)
值域
R(实数集)
奇偶性
奇函数
单调性
当k>0时,图像位于第一、三象限,从左往右,y随x的增大而增大(单调递增),为增函数;
当k<0时,图像位于第二、四象限,从左往右,y随x的增大而减小(单调递减),为减函数。
周期性
不是周期函数。
对称性
对称点:关于原点成中心对称
对称轴:自身所在直线;自身所在直线的垂直平分线
图象:一条经过原点的直线。
性质:
(1)当k>0时,y随x的增大而增大;
(2)当k<0时,y随x的增大而减小。
1、在x允许的范围内取一个值,根据解析式求出y的值;
2、根据第一步求的x、y的值描出点;
3、作出第二步描出的点和原点的直线(因为两点确定一直线)。
正比例函数的图像: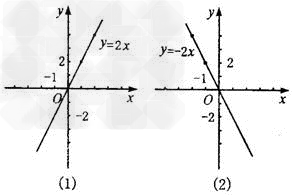
一次函数的定义:
在某一个变化过程中,设有两个变量x和y,如果可以写成y=kx+b(k、b为常数,k≠0),那么我们就说y是x的一次函数,其中x是自变量,y是因变量。
①正比例函数是一次函数,但一次函数不一定是正比例函数;
②一般情况下,一次函数的自变量的取值范围时全体实数;
③如果一个函数是一次函数,则含有自变量x的式子是一次的,系数k不等于0,而b可以为任意实数。
一次函数基本性质:
1.在正比例函数时,x与y的商一定(x≠0)。在反比例函数时,x与y的积一定。
在y=kx+b(k,b为常数,k≠0)中,当x增大m时,函数值y则增大km,反之,当x减少m时,函数值y则减少km。
2.当x=0时,b为一次函数图像与y轴交点的纵坐标,该点的坐标为(0,b)。
3.当b=0时,一次函数变为正比例函数。当然正比例函数为特殊的一次函数。
4.在两个一次函数表达式中:
当两个一次函数表达式中的k相同,b也相同时,则这两个一次函数的图像重合;
当两个一次函数表达式中的k相同,b不相同时,则这两个一次函数的图像平行;
当两个一次函数表达式中的k不相同,b不相同时,则这两个一次函数的图像相交;
当两个一次函数表达式中的k不相同,b相同时,则这两个一次函数图像交于y轴上的同一点(0,b);
当两个一次函数表达式中的k互为负倒数时,则这两个一次函数图像互相垂直。
5.两个一次函数(y1=k1x+b1,y2=k2x+b2)相乘时(k≠0),得到的的新函数为二次函数,
该函数的对称轴为-(k2b1+k1b2)/(2k1k2);
当k1,k2正负相同时,二次函数开口向上;
当k1,k2正负相反时,二次函数开口向下。
二次函数与y轴交点为(0,b2b1)。
6.两个一次函数(y1=ax+b,y2=cx+d)之比,得到的新函数y3=(ax+b)/(cx+d)为反比例函数,渐近线为x=-b/a,y=c/a。
一次函数的判定:
①判断一个函数是否是一次函数,就是判断它是否能化成y=kx+b的形式;
②当k≠0,b=0时,这个函数即是k≠0一次函数,k≠0又是正比例函数;
③当k=0,b≠0时,这个函数不是一次函数;
④一次函数的一般形式是关于x的一次二项式,它可以转化为含x、y的二元一次方程。
在某一个变化过程中,设有两个变量x和y,如果可以写成y=kx+b(k、b为常数,k≠0),那么我们就说y是x的一次函数,其中x是自变量,y是因变量。
①正比例函数是一次函数,但一次函数不一定是正比例函数;
②一般情况下,一次函数的自变量的取值范围时全体实数;
③如果一个函数是一次函数,则含有自变量x的式子是一次的,系数k不等于0,而b可以为任意实数。
一次函数基本性质:
1.在正比例函数时,x与y的商一定(x≠0)。在反比例函数时,x与y的积一定。
在y=kx+b(k,b为常数,k≠0)中,当x增大m时,函数值y则增大km,反之,当x减少m时,函数值y则减少km。
2.当x=0时,b为一次函数图像与y轴交点的纵坐标,该点的坐标为(0,b)。
3.当b=0时,一次函数变为正比例函数。当然正比例函数为特殊的一次函数。
4.在两个一次函数表达式中:
当两个一次函数表达式中的k相同,b也相同时,则这两个一次函数的图像重合;
当两个一次函数表达式中的k相同,b不相同时,则这两个一次函数的图像平行;
当两个一次函数表达式中的k不相同,b不相同时,则这两个一次函数的图像相交;
当两个一次函数表达式中的k不相同,b相同时,则这两个一次函数图像交于y轴上的同一点(0,b);
当两个一次函数表达式中的k互为负倒数时,则这两个一次函数图像互相垂直。
5.两个一次函数(y1=k1x+b1,y2=k2x+b2)相乘时(k≠0),得到的的新函数为二次函数,
该函数的对称轴为-(k2b1+k1b2)/(2k1k2);
当k1,k2正负相同时,二次函数开口向上;
当k1,k2正负相反时,二次函数开口向下。
二次函数与y轴交点为(0,b2b1)。
6.两个一次函数(y1=ax+b,y2=cx+d)之比,得到的新函数y3=(ax+b)/(cx+d)为反比例函数,渐近线为x=-b/a,y=c/a。
一次函数的判定:
①判断一个函数是否是一次函数,就是判断它是否能化成y=kx+b的形式;
②当k≠0,b=0时,这个函数即是k≠0一次函数,k≠0又是正比例函数;
③当k=0,b≠0时,这个函数不是一次函数;
④一次函数的一般形式是关于x的一次二项式,它可以转化为含x、y的二元一次方程。
发现相似题
与“如图,点A的坐标为(-1,0),点B在直线y=x上运动,当线段AB最...”考查相似的试题有:
- 我们知道,随着海拔高度的上升,温度随之下降,且温度y(℃)是高出地面(千米)的一次函数.南通气象台某仪器显示,某时刻高...
- 直线与轴、轴所围成的三角形的面积为()A.3B.6C.D.
- 为弘扬体育精神,锻炼师生体魄,我校组织了今年春季运动会.在男子100米预赛中,高二年级某同学甲在发令枪响的同时立即起跑,...
- 已知函数(1)画出这个函数的图象;(2)写出这个函数的图象与x轴,y轴的交点坐标(3)求此函数的图象与坐标轴围成的三角形的...
- 一次函数(k为常数且)的图象如图所示,则使y>0成立的x的取值范围为 .
- 如图,已知直线l1:y=k1x+4与直线l2:y=k2x﹣5交于点A,它们与y轴的交点分别为点B,C,点E,F分别为线段AB、AC的中点,则线段...
- 某部队甲、乙两班参加植树活动.乙班先植树30棵,然后甲班才开始与乙班一起植树.设甲班植树的总量为y甲(棵),乙班植树的总量...
- 张师傅驾车从甲地到乙地,两地相距500千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以100千米/小时的速度...
- 一次函数的图象经过的象限是( )A.一、二、三B.二、三、四C.一、二、四D.一、三、四
- 小敏家距学校米,某天小敏从家里出发骑自行车上学,开始她以每分钟米的速度匀速行驶了米,遇到交通堵塞,耽搁了分钟,然后以...