本试题 “如图1,BD、CE分别是△ABC的外角平分线,过点A作AF⊥BD,AG⊥CE,垂足分别为F、G,连接FG,延长AF、AG,与直线BC相交于M、N.(1)试说明:FG=12(AB+BC+AC);...” 主要考查您对三角形中位线定理
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 三角形中位线定理
三角形中位线定义:
连接三角形两边中点的线段叫做三角形的中位线。一个三角形共有三条中位线。
三角形中位线定理:
三角形的中位线平行于第三边,并且等于它的一半。

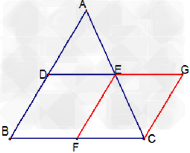
如图已知△ABC中,D,E分别是AB,AC两边中点。
则DE平行于BC且等于BC/2
三角形中位线逆定理:
逆定理一:在三角形内,与三角形的两边相交,平行且等于三角形第三边一半的线段是三角形的中位线。
如图DE//BC,DE=BC/2,则D是AB的中点,E是AC的中点。
逆定理二:在三角形内,经过三角形一边的中点,且与另一边平行的线段,是三角形的中位线。
如图D是AB的中点,DE//BC,则E是AC的中点,DE=BC/2
区分三角形的中位线和中线:
三角形的中位线是连结三角形两边中点的线段;
三角形的中线是连结一个顶点和它的对边中点的线段。
连接三角形两边中点的线段叫做三角形的中位线。一个三角形共有三条中位线。
三角形中位线定理:
三角形的中位线平行于第三边,并且等于它的一半。

如图已知△ABC中,D,E分别是AB,AC两边中点。
则DE平行于BC且等于BC/2
三角形中位线逆定理:

逆定理一:在三角形内,与三角形的两边相交,平行且等于三角形第三边一半的线段是三角形的中位线。
如图DE//BC,DE=BC/2,则D是AB的中点,E是AC的中点。
逆定理二:在三角形内,经过三角形一边的中点,且与另一边平行的线段,是三角形的中位线。
如图D是AB的中点,DE//BC,则E是AC的中点,DE=BC/2
区分三角形的中位线和中线:
三角形的中位线是连结三角形两边中点的线段;
三角形的中线是连结一个顶点和它的对边中点的线段。
发现相似题
与“如图1,BD、CE分别是△ABC的外角平分线,过点A作AF⊥BD,AG⊥CE...”考查相似的试题有:
- 如图,已知点D、E、F分别是△ABC三边的中点,△DEF的周长为20cm,则△ABC的周长为______cm.
- 下列命题中,错误的是[ ]A.三角形两边之和大于第三边B.三角形的外角和等于360°C.三角形的一条中线能将三角形面积分成相等...
- a、b、c是△ABC的三边,且a=7,b=11,第三边c能被5整除,则c的长为( )。
- 以△ABC的两边AB、AC为腰分别向外作等腰Rt△ABD和等腰Rt△ACE,∠BAD=∠CAE=90°,连接DE,M、N分别是BC、DE的中点探究:AM与DE 的...
- 如图,四边形ABCD的两条对角线AC、BD互相垂直,A1B1C1D1是四边形ABCD的中点四边形,如果AC=8,BD=10,那么四边形A1B1C1D1的面...
- 如图,A,B两点被池塘隔开,在AB外选一点C,连接AC和BC,并分别找出它们的中点M,N.若测得MN=15m,则A,B两点间的距离为( ...
- 如果顺次连接四边形各边中点所围成的四边形是矩形,那么原来的四边形一定是( ) A.平行四边形 B.梯形 C.对角线相等的四边...
- 如图,E、F是△ABC两边的中点,若EF=3,则BC=( )。
- 如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,若AD=8cm,则OE的长为( )cm。
- 如图,D是△ABC内一点,AD=6,BC=4,E,F,G,H分别是AB,AC,CD,BD的中点,则四边形EFGH的周长是( )A.7B.9C.10D.11