本试题 “平面向量a与b的夹角为60°且|a|=2,|b|=1,则向量a+2b的模为( )A.23B.12C.32D.10” 主要考查您对向量数量积的含义及几何意义
向量模的计算
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 向量数量积的含义及几何意义
- 向量模的计算
两个向量的夹角的定义:
对于非零向量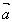 ,
,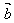 ,作
,作 称为向量
称为向量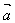 ,
,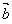 的夹角,当
的夹角,当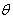 =0时,
=0时,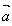 ,
,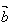 同向,当
同向,当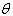 =π时,
=π时,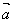 ,
,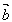 反向,
反向,
当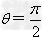 时,
时,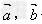 垂直。
垂直。
两个向量数量积的含义:
如果两个非零向量 ,
, ,它们的夹角为
,它们的夹角为 ,我们把数量
,我们把数量 叫做
叫做 与
与 的数量积(或内积或点积),记作:
的数量积(或内积或点积),记作: ,即
,即 。
。 叫
叫 在
在 上的投影。
上的投影。
规定:零向量与任一向量的数量积是0,注意数量积是一个实数,不再是一个向量。
两个向量数量积的几何意义:
数量积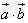 等于
等于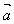 的模
的模 与
与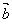 在
在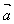 上的投影
上的投影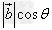 的乘积。
的乘积。
向量数量积的性质:
设两个非零向量
(1) ;
;
(2) ;
;
(3) ;
;
(4) ;
;
(5)当 ,
, 同向时,
同向时, ;当
;当 与
与 反向时,
反向时, ;当
;当 为锐角时,
为锐角时, 为正且
为正且 ,
, 不同向,
不同向, ;当
;当 为钝角时,
为钝角时, 为负且
为负且 ,
, 不反向,
不反向, 。
。
向量的模:
设 ,则有向线段
,则有向线段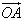 的长度叫做向量
的长度叫做向量 的长度或模,记作:
的长度或模,记作: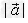 ,则
,则  。
。
向量模的坐标表示:
(1)若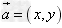 ,则
,则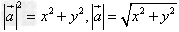 ;
;
(2)若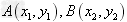 ,那么
,那么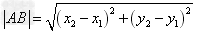 。
。
求向量的模:
求向量的模主要是利用公式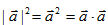 来解。
来解。
发现相似题
与“平面向量a与b的夹角为60°且|a|=2,|b|=1,则向量a+2b的模为(...”考查相似的试题有:
- 如图,空间四边形OABC中,,,,点M在OA上,且,N为BC的中点,则等于( )A.B.C.D.
- 已知和点M,对空间内的任意一点满足,,若存在实数m使得,则m=( )A.2B.3C.4D.5
- 已知向量、b的夹角为π3,|a|=2,|b|=1,且a⊥(a-mb),那么实数m=______.
- 如图,在四边形ABCD中,,则的值为( )A.2B.C.4D.
- 在ABCD中,错误的式子是( ) A.B.C.D.
- 已知,,,,则的最大值为( )A.B. 2C.D.
- 已知=,=1,=1,则向量与的夹角为A.B.C.D.
- 已知单位向量e1,e2的夹角为60°,则|2e1-e2|=______.
- 已知向量a=(-2,2),b=(5,k),若|a+b|不超过5,则k的取值范围是( )A.[-4,6]B.[-6,4]C.[-6,2]D.[-2,6]
- 在锐角△ABC中,已知角A、B、C所对的边分别为a,b,c,且tanA-tanB=(1+tanAtanB),(1)若c2=a2+b2-ab,求角A、B、C的大小;(2)...