本试题 “一条弦把圆的一条直径分成2cm和6cm两部分,若弦与直径所成的角为30°,则圆心到弦的距离为______.” 主要考查您对直角三角形的性质及判定
垂直于直径的弦
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 直角三角形的性质及判定
- 垂直于直径的弦
有一个角为90°的三角形,叫做直角三角形。直角三角形可用Rt△表示,如直角三角形ABC写作Rt△ABC。
直角三角形性质:
直角三角形是一种特殊的三角形,它除了具有一般三角形的性质外,具有一些特殊的性质:
性质1:直角三角形两直角边a,b的平方和等于斜边c的平方。即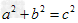 。如图,∠BAC=90°,则AB2+AC2=BC2(勾股定理)
。如图,∠BAC=90°,则AB2+AC2=BC2(勾股定理)
性质2:在直角三角形中,两个锐角互余。如图,若∠BAC=90°,则∠B+∠C=90°
性质3:在直角三角形中,斜边上的中线等于斜边的一半(即直角三角形的外心位于斜边的中点,外接圆半径R=C/2)。
性质4:直角三角形的两直角边的乘积等于斜边与斜边上高的乘积。
性质5:
如图,Rt△ABC中,∠BAC=90°,AD是斜边BC上的高,则有射影定理如下:
(1)(AD)2=BD·DC。
(2)(AB)2=BD·BC。
(3)(AC)2=CD·BC。
性质6:在直角三角形中,如果有一个锐角等于30°,那么它所对的直角边等于斜边的一半。
在直角三角形中,如果有一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°。
性质7:如图,1/AB2+1/AC2=1/AD2
性质8:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。
性质9:直角三角形直角上的角平分线与斜边的交点D 则 BD:DC=AB:AC
直角三角形的判定方法:
判定1:定义,有一个角为90°的三角形是直角三角形。
判定2:判定定理:以a、b、c为边的三角形是以c为斜边的直角三角形。如果三角形的三边a,b,c满足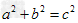 ,那么这个三角形就是直角三角形。(勾股定理的逆定理)。
,那么这个三角形就是直角三角形。(勾股定理的逆定理)。
判定3:若一个三角形30°内角所对的边是某一边的一半,则这个三角形是以这条长边为斜边的直角三角形。
判定4:两个锐角互为余角(两角相加等于90°)的三角形是直角三角形。
判定5:若两直线相交且它们的斜率之积互为负倒数,则两直线互相垂直。那么
判定6:若在一个三角形中一边上的中线等于其所在边的一半,那么这个三角形为直角三角形。
判定7:一个三角形30°角所对的边等于这个三角形斜边的一半,则这个三角形为直角三角形。(与判定3不同,此定理用于已知斜边的三角形。)
垂径定理:
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。
注:
(1)定理中的直径过圆心即可,可以是直径、半径、过圆心的直线或线段;
(2)此定理是证明等线段、等角、垂直的主要依据,同时也为圆的有关计算提供了方法和依据。
垂径定理的推论:
推论一:平分弦(不是直径)的直径垂直于这条弦,并且平分这条弦所对的两段弧
推论一:平分弦(不是直径)的直径垂直于这条弦,并且平分这条弦所对的两段弧
推论二:弦的垂直平分线经过圆心,并且平分这条弦所对的弧
推论三:平分弦所对的一条弧的直径垂直平分这条弦,并且平分这条弦所对的另一条弧
推论四:在同圆或者等圆中,两条平行弦所夹的弧相等
(证明时的理论依据就是上面的五条定理)
但是在做不需要写证明过程的题目中,可以用下面的方法进行判断:
一条直线,在下列5条中只要具备其中任意两条作为条件,就可以推出其他三条结论
1.平分弦所对的优弧
2.平分弦所对的劣弧
(前两条合起来就是:平分弦所对的两条弧)
3.平分弦 (不是直径)
4.垂直于弦
5.经过圆心
与“一条弦把圆的一条直径分成2cm和6cm两部分,若弦与直径所成的...”考查相似的试题有:
- 将一副三角尺如图所示叠放在一起,若AB=14cm,则阴影部分的面积是( )cm2。
- 已知点A和点B,以点A和点B为两个顶点作等腰直角三角形,则一共可作出( )A.3个B.4个C.6个D.7个
- 正方形ABCD的边长与等腰直角三角形PMN的腰长均为4cm,且AB与MN都在直线l上,开始时点B与点M重合.让正方形沿直线向右平移,直...
- 已知:如图,△ABC是边长3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当...
- 如图,一个含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到△A′B′C的位置,若BC的长为15cm,那么AA’的长为( ...
- 如图,在由边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,E为BC中点,请按要求完成下列各题:(1)画AD∥BC(D为...
- 如图,AB是⊙O的直径,AB⊥CD于E,AB=10,CD=8,则BE为( )A.2B.3C.4D.3.5
- 已知AD是△ABC的高,AB=4,AC=3,AD=2,则△ABC的外接圆的直径是( ) A.2 B.4 C.6 D.8
- 如图,在⊙O中,直径MN垂直于弦AB,垂足为C,下面结论中错误是( ) A.AC=BC B. C. D.OC=CN
- 如图,AB是⊙O的直径,且AB=10,弦MN的长是6,若弦MN的两端在圆上滑动,始终与AB相交,设点A、B到MN的距离分别为h1,h2,则|h1...