本试题 “甲、乙两个仓库存粮总数是80吨,其中甲仓库存粮的与乙仓库的相等,两个仓库各存粮多少吨?” 主要考查您对比例的意义,比例的基本性质
解比例,比例的应用题
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 比例的意义,比例的基本性质
- 解比例,比例的应用题
表示两个比相等的式子叫做比例。
比例的基本性质:
组成比例的四个数,叫做比例的项。两端的两项叫做比例的外项,中间的两项叫做比例的内项。
在比例里,两个外项的积等于两个内项的积。
用字母表示为:如果  (a,b, c,d 都不等于零),那么ad=bc.
(a,b, c,d 都不等于零),那么ad=bc.
这是因为用bd去乘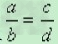 的两边,得
的两边,得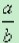 ?bd=
?bd= ?bd,所以ad=bc.
?bd,所以ad=bc.
性质推论:
从比例的这个基本性质,可以推得:
如果两个数的积等于另外两个数的积,那么这四个数可以组成比例。
用式子表示就是:如果ad=bc,那么 (b.d都不等于零)。
(b.d都不等于零)。
这是因为用bd 去除ad=bc两边,得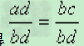 ,所以
,所以 。
。
比例意义:
正比例的意义:
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做成正比例关系。
正比例关系两种相关联的量的变化规律:同时扩大,同时缩小,比值不变。
反比例的意义:
成反比例的量包括三个数量,一个定量和两个变量。研究两个变量之间的扩大(或缩小)的变化关系。一种量发生变化,引起另一种量发生相反的变化。这两种量是反比例的量,它们的关系成反比例关系。
反比例实质:
两种相关联的量,一种量变化,另一种量也随着变化,这两种量中相对应的两个数的积一定。这两种量叫做成反比例的量。它们的关系叫做反比例关系。
解比例:
求比例中的未知项,叫做解比例。
根据比例的基本性质(即交叉相乘),如果已知比例中的任何三项,就可以求出这个比例中的另外一个未知项。求比例中的未知项,叫做解比例。解比例是利用比例的基本性质:在比例中,两个外项的积等于两个内项的积。再转化成方程。
比例应用题:
是小学六年级奥数中的一个重要内容。它既是整数应用题的继续与深化,又是学习更多数学知识的重要基础,同时,这类题又有着自身的特点和解题的规律。在处理几个量的倍比关系时,比例应用题与分数百分数应用题间有很多相似之处,但利用比例处理问题要方便灵活得多。
要解决好此类问题,须注意灵活运用画线段示意图等手段,多角度、多侧面思考问题。在解题过程中,要善于掌握对应、假设、转化等多种解题方法,在寻找正确的解题方法的同时,不断地开拓解题思路。
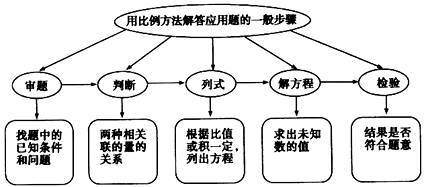
用比例方法解应用题的一般步骤:
与“甲、乙两个仓库存粮总数是80吨,其中甲仓库存粮的与乙仓库的...”考查相似的试题有:
- 已知比例的一个内项是15比另一个内项多14,一个外项是18,另一个外项是______.
- 如果5a=8b(a、b均不为0),那么______:______=______:______.
- 一辆汽车从甲地到乙地要行480千米,前3小时行180千米,照这样计算,行完全程需要多少小时?(用比例方法解)
- 学校用同样的方砖铺地,铺地5平方米需要方砖120块,照这样计算,再铺32平方米,一共需要用这种方砖多少块?(用比例解)
- 甲数的56与乙数的45相等,则甲数大于乙数.______.
- B1大牛和小牛的头数比是4:5,表示大牛比小牛少15______.E1
- 一套西服的制作成本是266元,其中上衣和裤子制作成本的比是5:2.一件上衣的成本比一条裤子多多少元?
- 小明带一些钱去买练习本,如果0.6元一本,可以买8本,如果0.4元一本,可以买几本?
- 用24厘米的铁丝围成一个直角三角形,这个三角形三条边长度的比是3:4:5,这个直角三角形斜边上的高是______厘米.
- 改正下面的解比例算式。(1)5:2=9:x 改正:解:2x=9×5 x= x=22.5(2)x:1.2=0.5:2 改正:解:0.5x=1.2×2 x= x= 4.8