一元二次不等式的概念:
只含有一个未知数,并且未知数的最高次数是2 的不等式称为一元二次不等式.
一元二次不等式的解集:
使某个一元二次不等式成立的x的值叫做这个一元二次不等式的解,一元二次不等式的所有解组成的集合叫做这个一元二次不等式的解集。
同解不等式:
如果两个不等式的解集相同,那么这两个不等式叫做同解不等式,如果一个不等式变形为另一个不等式时,这两个不等式是同解不等式,那么这种变形叫做不等式的同解变形。
二次函数的图象、一元二次方程的根、一元二次不等式的解集间的关系:
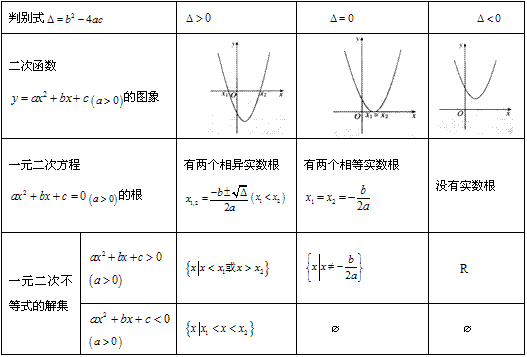
解不等式的过程:
解不等式的过程就是将不等式进行同解变形,化为最简形式的同解不等式的过程.变形时要注意条件的限制,比如:分母是否有意义,定义域是否有限制等.
解一元二次不等式的一般步骤为:
(1)对不等式变形,使一端为零且二次项系数大于零;(2)计算相应的判别式;(3)当△≥0时,求出相应的一元二次方程的根;(4)根据二次函数图象写出一元二次不等式的解集.
解含有参数的一元二次不等式:
(1)要以二次项系数与零的大小作为分类标准进行分类讨论;(2)转化为标准形式的一元二次不等式(即二次项系数大于零)后,再以判别式与零的大小作为分类标准进行分类讨论;(3)如果判别式大于零,但两根的大小还不能确定,此时再以两根的大小作为分类标准进行分类讨论。