本试题 “若某产品的直径长与标准值的差的绝对值不超过1mm 时,则视为合格品,否则视为不合格品.在近期一次产品抽样检查中,从某厂生产的此种产品中,随机抽取5000件...” 主要考查您对频率分布表、频率分布直方图、频率分布折线图、茎叶图
用样本估计总体
几何概型的定义及计算
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 频率分布表、频率分布直方图、频率分布折线图、茎叶图
- 用样本估计总体
- 几何概型的定义及计算
频率分布:
样本中所有数据(或者数据组)的频率和样本容量的比就是该数据的频率,所有数据(或者数据组)的频率的分布变化规律叫做频率分布,可以用频率分布表,频率分布折线图,茎叶图,频率分布直方图来表示.
频率分布折线图:
如果将频率分布直方图中各相邻的矩形的上底边的中点顺次连接起,就得到一条折线,称这条折线为本组数据的频率折线图。
频数分布表:
反映总体频率分布的表格。
一般地,编制频率分布表的步骤如下:(1)求全距,决定组数和组距;(2)分组,通常对组内数值所在区间取左闭右开区间,最后一组取闭区间;(3)登记频数,计算频率,列出频率分布表。
茎叶图:
(1)茎是指中间的一列数,叶是从茎的旁边生长出来的数。
(2)制作茎叶图的方法是:将所有两位数的十位数字作为“茎”,个位数字作为“叶”,茎相同者共用一个茎,茎按从小到大的顺序从上向下列出,共茎的叶一般按从大到小(或从小到大)的顺序同行列出;
(3)茎叶图的性质: ①茎叶图的优点是保留了原始数据,便于记录及表示,能反映数据在各段上的分布情况。
②茎叶图不能直接反映总体的分布情况,这就需要通过茎叶图给出的数据求出数据的数字特征,进一步估计总体情况。
茎叶图的性质:
①茎叶图的优点是保留了原始数据,便于记录及表示,能反映数据在各段上的分布情况。
②茎叶图不能直接反映总体的分布情况,这就需要通过茎叶图给出的数据求出数据的数字特征,进一步估计总体情况。
作频率分布直方图的步骤:
①求极差,即一组数据中最大值和最小值的差。
②决定组距与组数.将数据分组时,组数应力求合适,以使数据的分布规律能较清楚的呈现出来。这时应注意:a.一般样本容量越大,所分组数越多;b.为方便起见,组距的选择应力求“取整”;c.当样本容量不超过100时,按照数据的多少,通常分成5组~l2组.
③将数据分组.
④计算各小组的频率(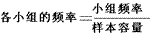 ),作频率分布表。
),作频率分布表。
⑤画频率分布直方图。
样本估计总体的定义:
用样本的频率分布去估计总体的频率分布就是用样本估计总体。
用样本估计总体的特点:
用样本估计总体时,样本容量越大,样本对总体的估计也就越精确。相应地,搜集、整理、计算数据的工作量也就越大,随机抽样是经过数学证明了的可靠的方法,它对于估计总体特征是很有帮助的.
用样本估计总体方法总结:
用样本频率分布来估计总体分布的重点是频率分布表和频率分布直方图的绘制及用样本频率分布估计总体分布,在计数和计算时一定要准确,在绘制小矩形时,宽窄要一致,通过频率分布表和频率分布直方图可以对总体作出估计。
几何概型的概念:
如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)称比例,则称这样的概率模型为几何概率模型,简称为几何概型。
几何概型的概率:
一般地,在几何区域D中随机地取一点,记事件"该点落在其内部一个区域d内"为事件A,则事件A发生的概率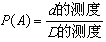 。
。
说明:(1)D的测度不为0;
(2)其中"测度"的意义依D确定,当D分别是线段,平面图形,立体图形时,相应的"测度"分别是长度,面积和体积;
(3)区域为"开区域";
(4)区域D内随机取点是指:该点落在区域内任何一处都是等可能的,落在任何部分的可能性大小只与该部分的测度成正比而与其形状位置无关.
几何概型的基本特点:
(1)试验中所有可能出现的结果(基本事件)有无限多个;
(2)每个基本事件出现的可能性相等.
与“若某产品的直径长与标准值的差的绝对值不超过1mm 时,则视为...”考查相似的试题有:
- (本小题满分12分)某市为了对学生的数理(数学与物理)学习能力进行分析,从10000名学生中随机抽出100位学生的数理综合学习...
- 为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:性别是否需要志愿者男...
- 为了保护环境,某校环保小组成员小沅收集废电池,第一天收集号电池节,号电池节,总质量为;第二天收集号电池节,号电池节,...
- 以下四个说法:①平均数不受少数几个极端值的影响,中位数受样本中的每一个数据影响;②同时抛掷两枚硬币,出现“两枚都是正面朝...
- 为了研究某高校大学新生的视力情况,随机地抽查了该校100名进校学生的视力情况,得到频率分布直方图如图所示,已知后6组的频...
- 驾驶员血液酒精浓度在20~80 mg/100 mL(不含80)之间,属酒后驾车,血液酒精浓度在80 mg/100 mL(含80)以上时,属醉酒驾车.市...
- 一个总体分为A,B两层,其个体数之比为4:1,用分层抽样方法从总体中抽取一个容量为10的样本.已知B层中甲、乙都被抽到的概率...
- 已知的平均数为a,标准差是b,则的平均数是__ __,标准差是____ __.
- 如图,在等腰直角三角形ABC中,在斜边AB上找一点M,则AM<AC的概率为( )A.22B.34C.23D.12
- 在区间[-π,π]内随机取两个数分别为a,b,则使得函数f(x)=x2+2ax-b2+π2有零点的概率为( )A.1-B.1-C.1-D.1-