如图，⊙O半径为2，直径CD以O为中心，在⊙O所在平面内转动，当CD 转动时，OA固定不动，0°≤∠DOA≤90°，且总有BC∥OA，AB∥,高中,数学试题,指数函数模型的应用考点,对数函数模型的应用考点,好技网

解答题
如图，⊙O半径为2，直径CD以O为中心，在⊙O所在平面内转动，当CD 转动时，OA固定不动，0°≤∠DOA≤90°，且总有BC∥OA，AB∥CD，若OA=4，BC与⊙O交于E，连AD，设CE为x，四边形ABCD的面积为y．
（1）求y关于x的函数解析式，并指出x的取值范围；
（2）当x=2
3
（3）时，求四边形ABCD在圆内的面积与四边形ABCD的面积之比；
（4）当x取何值时，四边形ABCD为直角梯形？连EF，此时OCEF变成什么图形？（只需说明结论，不必证明）．

本题信息：2004年上海模拟数学解答题难度较难来源:未知
本题答案
查看答案

本试题 “如图，⊙O半径为2，直径CD以O为中心，在⊙O所在平面内转动，当CD 转动时，OA固定不动，0°≤∠DOA≤90°，且总有BC∥OA，AB∥CD，若OA=4，BC与⊙O交于E，连AD，设CE为x...” 主要考查您对
指数函数模型的应用

对数函数模型的应用
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。

指数函数模型的应用
对数函数模型的应用

指数函数模型的定义：

恰当选择自变量将问题的目标表示成自变量的函数f（x）=a·b^x+c（a、b、c为常数，a≠0，b＞0，b≠1）的形式，进而结合指数函数的性质解决问题。

指数型复合函数的性质的应用:

(1)与指数函数有关的复合函数基本上有两类：
；②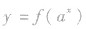.无论是哪一类，要搞清楚复合过程，才能确定复合函数的值域和单调区间，具体问题中，a的取值不定时，要对a进行分类讨论．
(2)对于形如一类的指数型复合函数，有以下结论：
①函数的定义域与f(x)的定义域相同；
②先确定函数f(x)的值域，再根据指数函数的值域、单调性，确定函数的值域；
③当a>l时，函数与函数f(x)的单调性相同；当O<a<l时，函数与函数f(x)的单调性相反.

对数函数模型的定义：

恰当选择自变量将问题的目标表示成自变量的函数f（x）=mlog_ax+n（m、n、a为常数，m≠0，a＞0，a≠1）的形式，进而结合对数函数的性质解决问题。

对数函数模型解析式：

f（x）=mlog_ax+n（m、n、a为常数，m≠0，a＞0，a≠1）

用函数模型解函数应用题的步骤：

1.审题：弄清题意，分清条件和结论，确定数量关系，初步选择数学模型；
2.建模：将自然语言转化为数学语言，将文字语言转化为符号语言，利用数学知识，建立相应的数学模型；
3.求模：求解数学模型，得出数学结论；
4.还原：将数学问题还原为实际问题的意义。

发现相似题

与“如图，⊙O半径为2，直径CD以O为中心，在⊙O所在平面内转动，当C...”考查相似的试题有：