本试题 “用配方法将二次函数y=2x2-4x-6化为y=a(x-h)2+k的形式(其中h,k为常数),并写出这个二次函数图象的顶点坐标和对称轴.” 主要考查您对二次函数的定义
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 二次函数的定义
定义:
一般地,如果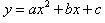 (a,b,c是常数,a≠0),那么y叫做x 的二次函数。
(a,b,c是常数,a≠0),那么y叫做x 的二次函数。
①所谓二次函数就是说自变量最高次数是2;
②二次函数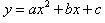 (a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时,
(a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时,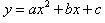 变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。
变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。
③二次函数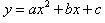 (a≠0)与一元二次方程
(a≠0)与一元二次方程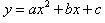 (a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
(a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式:
(1)一般式: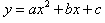 (a,b,c是常数,a≠0);
(a,b,c是常数,a≠0);
(2)顶点式: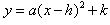 (a,h,k是常数,a≠0)
(a,h,k是常数,a≠0)
(3)当抛物线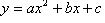 与x轴有交点时,即对应二次好方程
与x轴有交点时,即对应二次好方程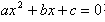 有实根x1和x2存在时,根据二次三项式的分解因式
有实根x1和x2存在时,根据二次三项式的分解因式 ,二次函数
,二次函数 可转化为两根式
可转化为两根式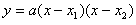 。如果没有交点,则不能这样表示。
。如果没有交点,则不能这样表示。
二次函数的一般形式的结构特征:
①函数的关系式是整式;
②自变量的最高次数是2;
③二次项系数不等于零。
二次函数的判定:
二次函数的一般形式中等号右边是关于自变量x的二次三项式;
当b=0,c=0时,y=ax2是特殊的二次函数;
判断一个函数是不是二次函数,在关系式是整式的前提下,如果把关系式化简整理(去括号、合并同类项)后,能写成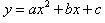 (a≠0)的形式,那么这个函数就是二次函数,否则就不是。
(a≠0)的形式,那么这个函数就是二次函数,否则就不是。
一般地,如果
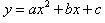 (a,b,c是常数,a≠0),那么y叫做x 的二次函数。
(a,b,c是常数,a≠0),那么y叫做x 的二次函数。 ①所谓二次函数就是说自变量最高次数是2;
②二次函数
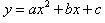 (a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时,
(a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时,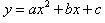 变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。
变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。③二次函数
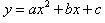 (a≠0)与一元二次方程
(a≠0)与一元二次方程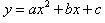 (a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
(a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。二次函数的解析式有三种形式:
(1)一般式:
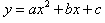 (a,b,c是常数,a≠0);
(a,b,c是常数,a≠0); (2)顶点式:
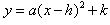 (a,h,k是常数,a≠0)
(a,h,k是常数,a≠0) (3)当抛物线
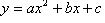 与x轴有交点时,即对应二次好方程
与x轴有交点时,即对应二次好方程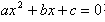 有实根x1和x2存在时,根据二次三项式的分解因式
有实根x1和x2存在时,根据二次三项式的分解因式 ,二次函数
,二次函数 可转化为两根式
可转化为两根式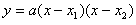 。如果没有交点,则不能这样表示。
。如果没有交点,则不能这样表示。 二次函数的一般形式的结构特征:
①函数的关系式是整式;
②自变量的最高次数是2;
③二次项系数不等于零。
二次函数的判定:
二次函数的一般形式中等号右边是关于自变量x的二次三项式;
当b=0,c=0时,y=ax2是特殊的二次函数;
判断一个函数是不是二次函数,在关系式是整式的前提下,如果把关系式化简整理(去括号、合并同类项)后,能写成
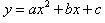 (a≠0)的形式,那么这个函数就是二次函数,否则就不是。
(a≠0)的形式,那么这个函数就是二次函数,否则就不是。 发现相似题
与“用配方法将二次函数y=2x2-4x-6化为y=a(x-h)2+k的形式(其中...”考查相似的试题有:
- 抛物线可以由抛物线向__________________(平移)得到.
- 抛物线y=(x+1)2+2的顶点在( )A.第一象限B.第二象限C.第三象限D.第四象限
- (12分)如图,在平面直角坐标系中,已知点A(-2,-4),OB=2,抛物线y=ax2+bx+c经过点A、O、B三点.(1)求抛物线的函数表达...
- 抛物线y=2x2-bx+3的对称轴是直线x=l,则b的值为 _______
- 如图,两条抛物线y1=-x2+1、y2=-x2-1 与分别经过点(-2,0),(2,0)且平行于y轴的两条平行线围成的阴影部分的面积为 ...
- 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:(1)4a+2b+c>0;(2)方程ax2+bx+c=0两根之和小于零;(3)y随...
- 把抛物线先向右平移1个单位,再向下平移2个单位,得到的抛物线的解析式为A.B.C.D.
- 已知二次函数的图象如图所示,给出以下结论:①;②当时,函数有最大值;③当时,函数y的值都等于0;④其中正确结论的个数是( )...
- 某公司经销一种绿茶,每千克成本为50元.市场调查发现,在一段时间内,销售量w(千克)随销售单价x(元/千克)的变化而变化,...
- 某商场购进一批单价为50元的商品,规定销售时单价不低于进价,每件的利润不超过40%.其中销售量y(件)与所售单价x(元)的关系可...