本试题 “设投掷1颗骰子的点数为ξ,则( ) A.Eξ=3.5,Dξ=3.52 B.Eξ=3.5,Dξ= C.Eξ=3.5,Dξ=3.5 D.Eξ=3.5,Dξ=” 主要考查您对离散型随机变量的期望与方差
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 离散型随机变量的期望与方差
数学期望的定义:
称 为ξ的数学期望或平均数,均值,数学期望又简称为期望,它反映了随机变量取值的平均水平。
为ξ的数学期望或平均数,均值,数学期望又简称为期望,它反映了随机变量取值的平均水平。
方差的定义:
称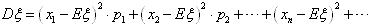 为ξ的均方差,简称为方差,
为ξ的均方差,简称为方差,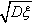 叫做随机变量ξ的标准差,记作:
叫做随机变量ξ的标准差,记作: 。
。
期望与方差的性质:
(1)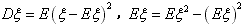 ;
;
(2)若η=aξ+b,则 ;
;
(3)若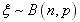 ,则
,则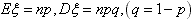 ;
;
(4)若ξ服从几何分布,则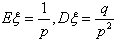 。
。
求均值(数学期望)的一般步骤:
(1)首先判断随机变量是否服从二点分布、二项分布或超几何分布,若服从,则直接用公式求均值.(2)若不服从特殊的分布,则先求出随机变量的分布列,再利用公式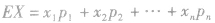 求均值。
求均值。
方差的求法:
(1)若随机变量X服从二点分布或二项分布,则直接利用方差公式可求.
(2)若随机变量X不服从特殊的分布时,求法为:
发现相似题
与“设投掷1颗骰子的点数为ξ,则( ) A.Eξ=3.5,Dξ=3.52 B.Eξ=...”考查相似的试题有:
- 把2对孪生兄弟共4人随机排成一排,记随机变量ξ为这一排中孪生兄弟相邻的对数,则随机变量ξ的期望Eξ=______.
- 某研究机构准备举办一次数学新课程研讨会,共邀请50名一线教师参加,使用不同版本教材的教师人数如下表所示版本人教A版人教B...
- 一个均匀小正方体的六个面中,三个面上标以数0,两个面上标以数1,一个面上标以数2,将这个小正方体抛掷2次,则向上的数之积的...
- 某体育课外兴趣小组共有15名成员,现有篮球班和排球班可供选择,其成员选择篮球班和排球班的数据如表所示:班类别篮球班排球...
- (理科)若随机变量ξ~N(2,22),则D(14ξ)的值为______.
- 某班同学利用寒假在三个小区进行了一次生活习惯进否符合低碳观念的调查.若生活习惯符合低碳观念的称为“低碳族”,否则称为“非...
- 抛掷两个骰子,至少有一个4点或5点出现时,就说这次试验成功,则在10次试验中,成功的次数X的期望是( )A.B.C.D.
- (本题满分14分)某学校某班文娱小组的每位组员唱歌、跳舞至少会一项,已知已知会唱歌的有2人,会跳舞听有5人,现从中选2人。...
- (本小题满分12分)2010年上海世博会大力倡导绿色出行,并提出在世博园区参观时可以通过植树的方式来抵消因出行产生的碳排放...
- 设集合,,分别从集合和中随机取一个数和.(1)若向量,,求向量与的夹角为锐角的概率;(2) 记点,则点落在直线上为事件,求使事件的...