已知函数y=a1-x（a＞0，a≠1）的图象恒过定点A，若点A在直线mx+ny-1=0（m＞0，n＞0）上，则的最小值为[ ]A．8B．9C,高中三年级,数学试题,指数函数的图象与性质考点,基本不等式及其应用考点,好技网

单选题
已知函数y=a^1-x（a＞0，a≠1）的图象恒过定点A，若点A在直线mx+ny-1=0（m＞0，n＞0）上，则的最小值为
[ ]

A．8
B．9
C．4
D．6

本题信息：2012年陕西省模拟题数学单选题难度一般来源:张玲玲
本题答案
查看答案

本试题 “已知函数y=a1-x（a＞0，a≠1）的图象恒过定点A，若点A在直线mx+ny-1=0（m＞0，n＞0）上，则的最小值为[ ]A．8B．9C．4D．6” 主要考查您对
指数函数的图象与性质

基本不等式及其应用
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。

指数函数的图象与性质
基本不等式及其应用

指数函数y=a^x（a＞0，且a≠1）的图象和性质：

		0<a<1	a>1
图像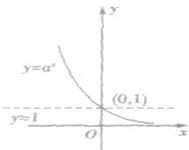
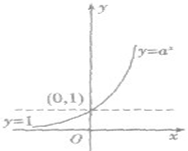图像	定义域	R
	值域	（0，+∞）
	恒过定点	图像恒过定点（0,1），即当x等于0时，y=1
	单调性	在（-∞，+∞）上是减函数	在（-∞，+∞）上是增函数
	函数值的变化规律	当x<0时，y>1	当x<0时，0<y<1
		当x=0时，y=1	当x=0时，y=1
		当x>0时，0<y<1	当x>0时，y>1

底数对指数函数的影响：

①在同一坐标系内分别作函数的图象，易看出：当a>l时，底数越大，函数图象在第一象限越靠近y轴；同样地，当0<a<l时，底数越小，函数图象在第一象限越靠近x轴．
②底数对函数值的影响如图．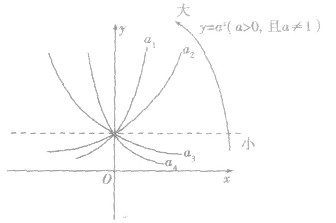

③当a>0，且a≠l时，函数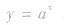与函数y=的图象关于y轴对称。

利用指数函数的性质比较大小：

若底数相同而指数不同，用指数函数的单调性比较：
若底数不同而指数相同，用作商法比较；
若底数、指数均不同，借助中间量，同时要注意结合图象及特殊值，

指数函数图象的应用：

函数的图象是直观地表示函数的一种方法．函数的很多性质，可以从图象上一览无余．数形结合就是几何与代数方法紧密结合的一种数学思想．指数函数的图象通过平移、翻转等变可得出一般函数的图象．利用指数函数的图象，可解决与指数函数有关的比较大小、研究单调性、方程解的个数、求值域或最值等问题．

基本不等式：

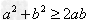（当且仅当a＝b时取“=”号）；
变式：①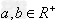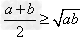，（当且仅当a＝b时取“=”号），即两个正数的算术平均不小于它们的几何平均。
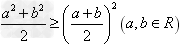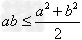②；③；④；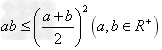

对基本不等式的理解：

(1)基本不等式的证明是利用重要不等式推导的，即，即有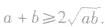
(2)基本不等式又称为均值定理、均值不等式等，其中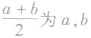的算术平均数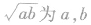，的几何平均数，本定理也可叙述为：两个正数的算术平均数不小于它们的几何平均数．
(3)要特别注意不等式成立的条件和等号成立的条件．均值不等式中：①当a=b时取等号，即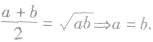

对于两个正数x，y，若已知xy，x+y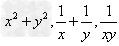，中的某一个为定值，可求出其余各个的最值：
如：（1）当xy＝P（定值），那么当x=y时，和x+y有最小值2，；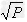
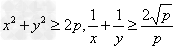（2）x+y=S（定值），那么当x=y时，积xy有最大值，；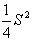
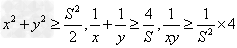（3）已知x²+y²=p，则x+y有最大值为，。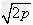

应用基本的不等式解题时：

注意创设一个应用基本不等式的情境及使等号成立的条件，即“一正、二定、三相等”。

利用基本不等式比较实数大小：

(1)注意均值不等式的前提条件．
(2)通过加减项的方法配凑成使用均值定理的形式．
(3)注意“1”的代换．
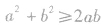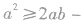
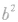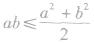(4)灵活变换基本不等式的形式，并注重其变形形式的运用．重要不等式的形式可以是，也可以是，还可以是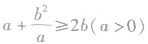等，不仅要掌握原来的形式，还要掌握它的几种变形形式以及公式的逆用等，以便应用．
(5)合理配组，反复应用均值不等式。

基本不等式的几种变形公式：

发现相似题

与“已知函数y=a1-x（a＞0，a≠1）的图象恒过定点A，若点A在直线mx...”考查相似的试题有：