本试题 “利用方格纸画图:(1)在下边的方格纸中,过C点画CD∥AB,过C点画CE⊥AB于E;(2)以CF为一边,画正方形CFGH,若每个小格的面积是1cm2,则正方形CFGH的面积是多少” 主要考查您对认识平面图形
平行线的判定
垂直的判定与性质
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 认识平面图形
- 平行线的判定
- 垂直的判定与性质
平面图形:
有些几何图形(如线段、角、三角形、长方形、圆等)的各个部分都在同一平面内,它们是平面图形。
如直线、射线、角、三角形、平行四边形、长方形(正方形)、梯形和圆都是几何图形,这些图形所表示的各个部分都在同一平面内,称为平面图形。
例如:有一组对边平行的四边形一定是平面图形。(两条平行线确定一个平面)
平面图形的大小,叫做它们的面积
点的形成是线,线的形成是面,面的形成是体。
平面图形分类:
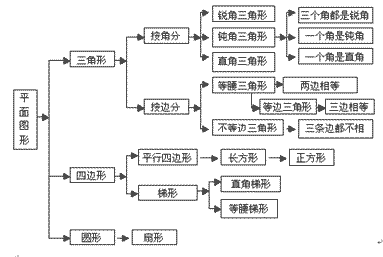
常见的平面图形图示:

从左到右依次为:长方形、正方形、三角形、圆、椭圆、
菱形、五边形、六边形。
几何图形知识体系图:
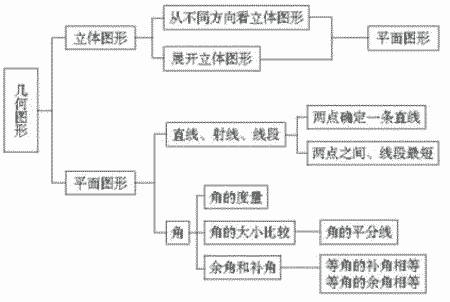
有些几何图形(如线段、角、三角形、长方形、圆等)的各个部分都在同一平面内,它们是平面图形。
如直线、射线、角、三角形、平行四边形、长方形(正方形)、梯形和圆都是几何图形,这些图形所表示的各个部分都在同一平面内,称为平面图形。
例如:有一组对边平行的四边形一定是平面图形。(两条平行线确定一个平面)
平面图形的大小,叫做它们的面积
点的形成是线,线的形成是面,面的形成是体。
平面图形分类:

常见的平面图形图示:

从左到右依次为:长方形、正方形、三角形、圆、椭圆、
菱形、五边形、六边形。
几何图形知识体系图:

平行线的概念:
在同一个平面内,不相交的两条直线叫做平行线。平行用符号“∥,如“AB∥CD”,读作“AB平行于CD”。
注意:
①平行线是无限延伸的,无论怎样延伸也不相交。
②当遇到线段、射线平行时,指的是线段、射线所在的直线平行。
在同一个平面内,不相交的两条直线叫做平行线。平行用符号“∥,如“AB∥CD”,读作“AB平行于CD”。
注意:
①平行线是无限延伸的,无论怎样延伸也不相交。
②当遇到线段、射线平行时,指的是线段、射线所在的直线平行。
平行线的判定平行线的判定公理:
(1)两条直线被第三条直线所截,如果同位角相等,那么两直线平行。简称:同位角相等,两直线平行。
(2)两条直线被第三条直线所截,如果内错角相等,那么两直线平行。简称:内错角相等,两直线平行。
(3)两条直线被第三条直线所截,如果同旁内角互补,那么两直线平行。简称:同旁内角互补,两直线平行。
还有下面的判定方法:
(1)平行于同一条直线的两直线平行。
(2)垂直于同一条直线的两直线平行。
(3)平行线的定义。
判定方法的逆应用:
在同一平面内,两直线不相交,即平行。
两条直线平行于一条直线,则三条不重合的直线互相平行。
两直线平行,同位角相等。
两直线平行,内错角相等。
两直线平行,同旁内角互补。
6a⊥c,b⊥c则a∥b。
垂线的定义:
两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直。其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足。
直线AB,CD互相垂直,记作“AB⊥CD”(或“CD⊥AB”),读作“AB垂直于CD”(或“CD垂直于AB”)。
垂线的性质:
性质1:过一点有且只有一条直线与已知直线垂直。
性质2:连结直线外一点与直线上各点的所有线段中,垂线段最短。简称:垂线段最短。
垂直的判定:垂线的定义。
两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直。其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足。
直线AB,CD互相垂直,记作“AB⊥CD”(或“CD⊥AB”),读作“AB垂直于CD”(或“CD垂直于AB”)。
垂线的性质:
性质1:过一点有且只有一条直线与已知直线垂直。
性质2:连结直线外一点与直线上各点的所有线段中,垂线段最短。简称:垂线段最短。
垂直的判定:垂线的定义。
发现相似题
与“利用方格纸画图:(1)在下边的方格纸中,过C点画CD∥AB,过C...”考查相似的试题有:
- 把四边形的任何一边向两方延长,如果其他各边都在延长线的同侧,这样的四边形叫做凸四边形.(1)如图,平面上线段AC、BD相交...
- 如图,已知四边形ABCD,根据以下步骤作图:(1)过点A作直线AE丄BC,E为垂足;(2)过点A作AF∥BC;(3)AE与∠B的平分线BF交于...
- 如图,直线a、b被直线c所截,下列说法正确的是( )A.当∠1=∠2时,一定有a∥bB.当a∥b时,一定有∠1=∠2C.当a∥b时,一定有∠1+∠2=18...
- 如图,已知直线EF和AB,CD分别相交于点K,H,且EG⊥AB,∠CHF=60°,∠E=30°,试证明:AB∥CD.
- 如图,在梯形ABCD中,,延长CD到点E,使DE=DA,连接AE.(1)求证:;(2)若AB=3,CD=1,求四边形ABCE的面积.
- 下列语句:①三条直线只有两个交点,则其中两条直线互相平行;②如果两条平行线被第三条截,同旁内角相等,那么这两条平行线都...
- 如图所示,请写出能判定CE∥AB的一个条件( ).
- 小颖正用一张半圆形纸片制作量角器模型.如图所示,AB是半圆的直径,点O是圆心.规定点A处的读数为180°,点B处的读数为0°,已...
- 如图,已知AB∥CD,∠AMP=150°,∠PND=60°,那么MP⊥PN吗?为什么?
- 如图,直线AB,CD相交于O点,OM?AB于O.(1)若∠1=∠2,求∠NOD;(2)若∠BOC=4∠1,求∠AOC与∠MOD.