本试题 “两个氘核聚变产生一个中子和一个氦核。已知氘核质量为2. 0136u ,氦核质量为3.0150u ,中子的质量为1.0087u 。(1) 写出聚变方程,求出释放能量(1u 相当于931...” 主要考查您对动量守恒定律的应用
轻核聚变
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 动量守恒定律的应用
- 轻核聚变
1、动量守恒定律:一个系统不受外力或者所受外力之和为零,这个系统的总动量保持不变。即m1v1+m2v2=m1v1'+m2v2'。
2、动量守恒定律的常见问题:
①碰撞问题;
②爆炸问题;
③反冲现象;
④人船模型;
“人船模型”是动量守恒定律的应用的一个经典模型,该模型应用的条件:一个原来处于静止状态的系统,当系统中的物体间发生相对运动的过程中,有一个方向上动量守恒。
⑤子弹打木块模型。
子弹打木块模型及推广:
Ⅰ、一物块在木板上滑动,μNS相对=ΔEk系统=Q,Q为摩擦在系统中产生的热量;
Ⅱ、小球在置于光滑水平面上的竖直平面内弧形光滑轨道上滑动,包括小车上悬一单摆单摆的摆动过程等。小球上升到最高点时系统有共同速度(或有共同的水平速度);系统内弹力做功时,不将机械能转化为其它形式的能,因此过程中系统机械能守恒。
Ⅲ、一静一动的同种电荷追碰运动等。
从“六性”把握动量守恒定律的应用方法:
1.条件性
动量守恒定律的成立是有条件的,只有当系统满足动量守恒的条件时才能利用方程式进行计算。
2.矢量性
动量守恒方程是一个矢量方程。对于作用前后物体的运动方向都在同一直线上的问题,应选取统一的正方向,凡是与选取正方向相同的动量为正,相反为负。若方向未知,可设为与正方向相同列动量守恒方程,通过解得结果的正负,判定未知量的方向。
3.参考系的同一性速度
具有相对性,公式中的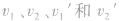 均应对同一参考系而言,一般均取对地的速度。
均应对同一参考系而言,一般均取对地的速度。
4.状态的同一性
相互作用前的总动量,这个“前”是指相互作用前的某一时刻,所以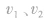 均是此时刻的瞬时速度,同理
均是此时刻的瞬时速度,同理 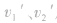 应是相互作用后的某一时刻的瞬时速度。
应是相互作用后的某一时刻的瞬时速度。
5.整体性
动量守恒定律是针对一个物体系统而言的,具有系统的整体性。
6.普适性
它不仅适用于两个物体所组成的系统,也适用于多个物体组成的系统;不仅适用于宏观物体组成的系统,也适用于微观粒子组成的系统。
临界与极值问题的解法:
在动量守恒定律的应用中,常常会遇到相互作用的两物体相距最近、避免相碰和物体开始反向运动等临界问题。分析临界问题的关键是寻找临界状态,临界状态的出现是有条件的,这种条件就是临界条件。临界条件往往表现为某个(或某些)物理量的特定取值。在与动量相关的临界问题中,临界条件常常表现为两物体的相对速度关系与相对位移关系,这些特定关系的判断是求解这类问题的关键。
“人船模型”的解题规律:
“人船模型”是动量守恒定律的拓展应用,它把速度和质量的关系推广到质量和位移的关系,这样给我们提供了一种解题思路和解决问题的方法。人船问题的适用条件是:两个物体组成的系统(当有多个物体组成系统时,可以先转化为两个物体组成的系统)动量守恒,系统的合动量为零。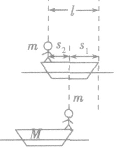
这种模型中涉及两种题型,一种题型是求解某物体在相互作用过程中通过的位移,此题型中需根据动量守恒、位移关系得到两个关系求解,如在图中,人从船头走到船尾时由动量守恒可得: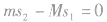
再由图中几何关系有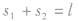
可得人船的位移分别为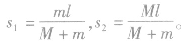
另一种题型是求某一时刻物体的速度,这种题型是先要由动量守恒求得两物体的一个速度关系,再由能量守恒得到两物体的另一个速度关系,从而求得物体的瞬时速度(或与瞬时速度相关的物理量)。
轻核裂变:
1、聚变:聚变把轻核合成质量较大的核,释放出核能的反应。
2、轻核的聚变: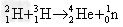 。
。
3、可控热核反应
①热核反应:使轻核发生聚变时,必须使它们的距离十分接近,达到10-15 m的近距离。所以可以通过高温(几百万摄氏度)剧烈的热运动使得一部分原子核已经具有足够的动能克服相互间的斥力,相互碰撞时发生聚变。可见聚变反应需要高温,所以又叫热核反应。
②可控热核反应与裂变相比的优点:释放能量大;无放射性物质;燃料丰富。
③太阳向外辐射大量的能量是靠太阳内部进行的热核反应产生的。
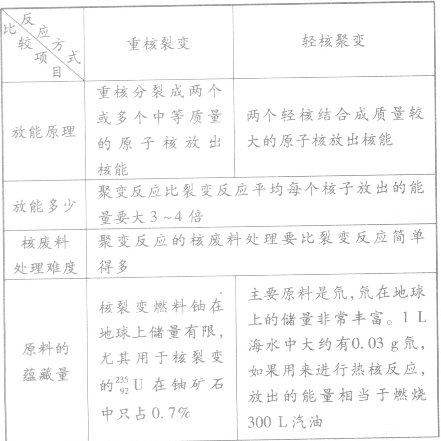
轻核聚变和重核裂变的对比:

与“两个氘核聚变产生一个中子和一个氦核。已知氘核质量为2. 0136...”考查相似的试题有:
- 质量为m的人站在质量为M、长为L的静止小船的右端,小船的左端靠在岸边(如图所示)。当他向左走到船的左端时,船左端离岸的距...
- 如图所示,木板A质量mA=1 kg,足够长的木板B质量mB=4 kg,质量为mC=2 kg的木块C置于木板B上,水平面光滑,B、C之间有摩擦。现...
- 设有钚的同位素离子静止在匀强磁场中,该离子沿与磁场垂直的方向放出α粒子以后,变成铀的一个同位素离子,同时放出能量为E=0....
- 两个氘核聚变产生一个中子和一个氦核。已知氘核质量为2. 0136u ,氦核质量为3.0150u ,中子的质量为1.0087u 。(1) 写出聚变方...
- 如图所示,设车厢长为L,质量为M,静止在光滑的水平面上。车厢内有一质量为m的物体以初速度v0向右运动,与车厢壁来回碰撞n次...
- 如图所示,以A、B和C、D为端点的两半圆形光滑轨道固定于竖直平面内,一滑板静止在光滑水平地面 上,左端紧靠B点,上表面所在...
- 如图所示,平板小车A放置于光滑水平面上,小滑块B以初速度v0=8m/s滑上平板小车左端,当B从小车右端滑出时,小车A的速度为1m/s...
- 重核的裂变和轻核的聚变是人类利用核能的两种主要方法,下面关于它们的说法中正确的是A.裂变和聚变过程都有质量亏损B.裂变...
- 下列说法正确的是( )A.α射线是高速运动的氦原子核B.核聚变反应方程 21H+ 31H→ 42He+ 10n中, 10n表示质子C.从金属表面逸...
- (2011年北京海淀区模拟)下列说法中正确的是( )A.天然放射现象的发现,揭示了原子的核式结构B.γ射线是波长很短的电磁波,它...