本试题 “(坐标系与参数方程选做题)在极坐标系中,过点(2,π4)作圆ρ=2的切线,则切线的直角坐标方程是______.” 主要考查您对简单曲线的极坐标方程
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 简单曲线的极坐标方程
曲线的极坐标方程的定义:
一般地,在极坐标系中,如果平面曲线C上任意一点的极坐标中至少有一个满足方程f(ρ,θ)=0,并且坐标适合方程f(ρ,θ)=0的点都在曲线上,那么方程f(ρ,θ)=0叫做曲线C的极坐标方程。
求曲线的极坐标方程的常用方法:
直译法、待定系数法、相关点法等。
圆心为(α,β)(a>0),半径为a的圆的极坐标方程为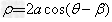 ,此圆过极点O。
,此圆过极点O。
直线的极坐标方程:
直线的极坐标方程是ρ=1/(2cosθ+4sinθ)。
圆的极坐标方程:

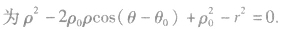

这是圆在极坐标系下的一般方程。
过极点且半径为r的圆方程:


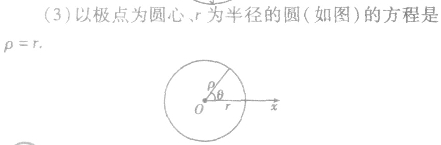
发现相似题
与“(坐标系与参数方程选做题)在极坐标系中,过点(2,π4)作圆ρ=...”考查相似的试题有:
- 极坐标方程4sinθ=5ρ表示的曲线是( ) A.圆 B.椭圆 C.双曲线的一支 D.抛物线
- 在极坐标系中,圆的圆心到直线的距离是_____________.
- 选修4-4:坐标系与参数方程已知极点与原点重合,极轴与x轴的正半轴重合.若曲线C1的极坐标方程为:5ρ2-3ρ2cos2θ-8=0,直线的...
- 在平面直角坐标系中,直线的参数方程为(为参数).若以坐标原点为极点,轴正半轴为极轴建立极坐标系,则曲线的极坐标方程为.(...
- (坐标系与参数方程选做题)在极坐标系中,直线截圆的弦长是在极坐标系中,直线截圆的弦长是( ).
- (选做题)在直角坐标系xOy中,直线l的参数方程为:(t为参数)在以O为极点,以x 轴的正半轴为极轴的极坐标系中,圆C的极坐标...
- 选修4-4:坐标系与参数方程已知圆锥曲线x=2cosθy=3sinθ(θ为参数)和定点A(0,3),F1,F2是左右焦点.(Ⅰ)求经过点F1垂直...
- (坐标系与参数方程选做题)在极坐标系中,点P(2,3π2)到直线l:3ρcosθ-4ρsinθ=3的距离为______.
- (极坐标与参数方程选作)在极坐标系中,圆的圆心到直线的距离为 .
- 已知曲线的极坐标方程为,直线的参数方程为 (为参数).、分别是曲线和直线上的任意一点,则的最小值为 .