本试题 “甲、乙两个篮球运动员互不影响地在同一位置上投球,命中率分别为13与p,且乙投球两次均为命中的概率为1625.(1)求乙投球的命中率p;(2)求甲投三次,至少...” 主要考查您对概率的基本性质(互斥事件、对立事件)
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 概率的基本性质(互斥事件、对立事件)
互斥事件:
事件A和事件B不可能同时发生,这种不可能同时发生的两个事件叫做互斥事件。
如果A1,A2,…,An中任何两个都不可能同时发生,那么就说事件A1,A2,…An彼此互斥。
对立事件:
两个事件中必有一个发生的互斥事件叫做对立事件,事件A的对立事件记做 。
。
注:两个对立事件必是互斥事件,但两个互斥事件不一定是对立事件。
事件A+B的意义及其计算公式:
(1)事件A+B:如果事件A,B中有一个发生发生。
(2)如果事件A,B互斥时,P(A+B)=P(A)+P(B),如果事件A1,A2,…An彼此互斥时,那么P(A1+A2+…+An)=P(A1)+P(A2)+…+P(An)。
(3)对立事件:P(A+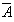 )=P(A)+P(
)=P(A)+P( )=1。
)=1。
概率的几个基本性质:
(1)概率的取值范围:[0,1].
(2)必然事件的概率为1.
(3)不可能事件的概率为0.
(4)互斥事件的概率的加法公式:
如果事件A,B互斥时,P(A+B)=P(A)+P(B),如果事件A1,A2,…An彼此互斥时,那么P(A1+A2+…+An)=P(A1)+P(A2)+…+P(An)。
如果事件A,B对立事件,则P(A+B)=P(A)+P(B)=1。
互斥事件与对立事件的区别和联系:
互斥事件是不可能同时发生的两个事件,而对立事件除要求这两个事件不同时发生外,还要求二者之一必须有一个发生。因此,对立事件是互斥事件的特殊情况,而互斥事件未必是对立事件,即“互斥”是“对立”的必要但不充分条件,而“对立”则是“互斥”的充分但不必要条件。
发现相似题
与“甲、乙两个篮球运动员互不影响地在同一位置上投球,命中率分...”考查相似的试题有:
- 下列说法正确的是A.互斥事件一定是对立事件,对立事件不一定是互斥事件B.互斥事件不一定是对立事件,对立事件一定是互斥事...
- 商场经销某商品,根据以往资料统计,顾客采用的付款期数的分布列为:12345P0.40.20.20.10.1商场经销一件该商品,采用1期付款...
- 某人身带钥匙3把(注3把钥匙中只有1把能打开家门),此人随机从口袋中摸出一把钥匙试开门.(1)开不了门不扔掉放回口袋继续...
- 已知事件M”3粒种子全部发芽”,事件N“3粒种子都不发芽”,那么事件M和N是( )A.互斥且对立事件B.不是互斥事件C.互斥但不对...
- 中国乒乓球队甲、乙两名队员参加奥运会乒乓球女子单打比赛,甲夺得冠军的概率为37,乙夺得冠军的概率为14,那么中国队夺得女...
- 随机地将编号为1,2,3,4的四个小球放入编号为1,2,3,4的四个盒子中,每个盒子放一个小球,事件“1号球放入1号盒子” 与事件“1号球...
- 根据以往统计资料,某地车主购买甲种保险的概率为0.5,购买乙种保险但不购买甲种保险的概率为0.3。设各车主购买保险相互独立...
- .若A与B是互斥事件,其发生的概率分别为,则A、B同时发生的概率为( )A. B. C. D. 0
- 一箱产品中有正品4件,次品3件,从中任取2件,其中事件:①恰有1件次品和恰有2件次品;②至少有1件次品和全是次品;③至少有1件...
- 同时掷3枚硬币,那么互为对立事件的是( )A.至少有1枚正面和最多有1枚正面B.最多1枚正面和恰有2枚正面C.至多1枚正面和至...