本试题 “已知下列命题:①相等的角是对顶角;②三角形三个内角的和等于180°;③互补的两个角一定是一个锐角,另一个为钝角;④平行于同一条直线的两条直线平行;⑤两直线平...” 主要考查您对余角,补角
相交线
三角形的内角和定理
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 余角,补角
- 相交线
- 三角形的内角和定理
余角:
如果两个角的和是一个直角,那么称这两个角互为余角,简称互余,也可以说其中一个角是另一个角的余角。
∠A +∠C=90°,∠A= 90°-∠C ,∠C的余角=90°-∠C 即:∠A的余角=90°-∠A
补角:
如果两个角的和是一个平角,那么这两个角叫互为补角.其中一个角叫做另一个角的补角
∠A +∠C=180°,∠A= 180°-∠C ,∠C的补角=180°-∠C 即:∠A的补角=180°-∠A
补角的性质:
同角的补角相等。比如:∠A+∠B=180°,∠A+∠C=180°,则:∠C=∠B。
等角的补角相等。比如:∠A+∠B=180°,∠D+∠C=180°,∠A=∠D则:∠C=∠B。
余角的性质:
同角的余角相等。比如:∠A+∠B=90°,∠A+∠C=90°,则:∠C=∠B。
等角的余角相等。比如:∠A+∠B=90°,∠D+∠C=90°,∠A=∠D则:∠C=∠B。
注意:
①钝角没有余角;
②互为余角、补角是两个角之间的关系。如∠A+∠B+∠C=90°,不能说∠A、∠B、∠C互余;同样:如∠A+∠B+∠C=180°,不能说∠A、∠B、∠C互为补角;
③互为余角、补角只与角的度数相关,与角的位置无关。只要它们的度数之和等于90°或180°,就一定互为余角或补角。
余角与补角概念认识提示:
(1)定义中的“互为”一词如何理解?
如果∠1与∠2互余,那么∠1的余角是∠2 ,同样∠2的余角是∠1 ;如果∠1与∠2互补,那么∠1的补角是∠2 , 同样∠2的补角是∠1。
(2)互余、互补的两角是否一定有公共顶点或公共边?
两角互余或互补,只与角的度数有关,与位置无关。
(3)∠1 + ∠2 + ∠3 = 90°(180°),能说∠1 、∠2、 ∠3 互余(互补)吗?
不能,互余或互补是两个角之间的数量关系。
相交线:
当两条不同的直线有一个公共点时,就称这两条直线相交,这个公共点叫做它们的交点。
当两条不同的直线有一个公共点时,就称这两条直线相交,这个公共点叫做它们的交点。
相交线性质: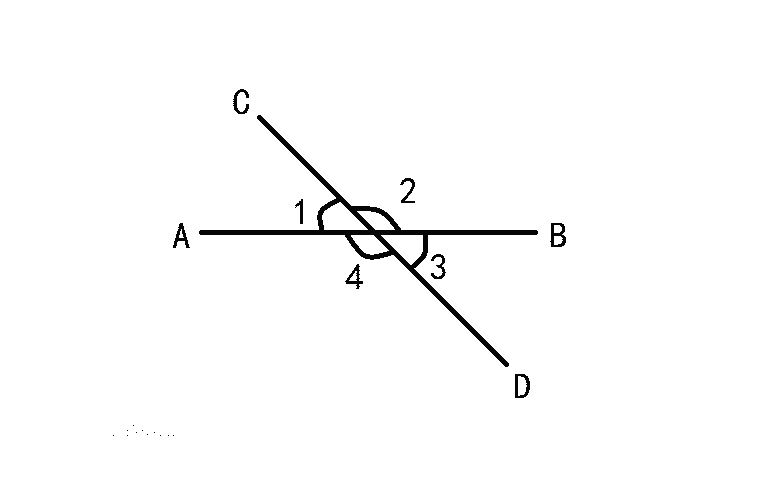
∠1和∠2有一条公共边OC,它们的另一边互为反向延长线(∠1和∠2互补),具有这种关系的两个角,互为邻补角。
∠1和∠3有一个公共顶点O,并且∠1的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角,互为对顶角。
∠1与∠2互补,∠3与∠2互补,由“同角的补角相等”,可以得出∠1=∠3.类似地,∠2=∠4.这样,
我们得到了对顶角的性质:对顶角相等。
垂线:
垂直是相交的一种特殊情形,两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足。
经过一点(已知直线上或直线外),能画出已知直线的一条垂线,并且只能画出一条垂线,即:
过一点有且只有一条直线与已知直线垂直。
连接直线外一点与直线上各点的所有线段中,垂线段最短.
简单说成:垂线段最短。
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
三角形的内角和定理及推论:
三角形的内角和定理:三角形三个内角和等于180°。
推论:
(1)直角三角形的两个锐角互余。
(2)三角形的一个外角等于和它不相邻的来两个内角的和。
(3)三角形的一个外角大于任何一个和它不相邻的内角。
注:在同一个三角形中:等角对等边;等边对等角;大角对大边;大边对大角。
三角形的内角和定理:三角形三个内角和等于180°。
推论:
(1)直角三角形的两个锐角互余。
(2)三角形的一个外角等于和它不相邻的来两个内角的和。
(3)三角形的一个外角大于任何一个和它不相邻的内角。
注:在同一个三角形中:等角对等边;等边对等角;大角对大边;大边对大角。
发现相似题
与“已知下列命题:①相等的角是对顶角;②三角形三个内角的和等于1...”考查相似的试题有:
- 如果一个角的余角和它的补角互补,那么这个角的度数为[ ]A.30°B.45°C.60°D.135°
- 一个角的补角与它的余角的度数之比是4:1,则这个角的度数是( )。
- 填空,完成下列说理过程.如图,BD平分∠ABC交AC于点D,∠C=∠DEB=90°,那么∠CDB与∠EDB相等吗?请说明理由.因为∠1+∠CDB+∠C=180°...
- 如图,已知∠AOC=90°,∠BOC 与∠COD 互补,∠COD=110°,求∠AOB 的度数。StartFragment
- 如图,CO⊥AB于点O,DE经过点O,∠COD=50°,则∠AOE为( )A.30oB.40oC.50oD.60o
- ∠A与∠B互为余角,∠A=35°,那么∠B的补角=______.
- 如图所示,∠DOF的对顶角是______.
- 若∠1的对顶角是∠2,∠2的邻补角是∠3,∠3=45°,则∠1的度数为______.
- 等腰三角形中有一个角等于50°,则另外两个角的度数为______.
- 如图,AF是BC边上的高,AD是∠BAC的平分线,∠B=36°,∠C=76°,那么△ADF的三个内角分别是( )、( )、( )。