本试题 “一个圆柱和一个圆锥高相等，它们底面积的比是3：1，它们体积的比是[ ]A．1：3B．3：1C．9：1D．1：1” 主要考查您对比的应用
圆柱的体积
圆锥的体积
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 比的应用
- 圆柱的体积
- 圆锥的体积
比的应用:
根据各部分的比，确定各部分与总量之间的关系，即各部分占总量的几分之几，然后按照“求一个数（这里指分配的量）的几分之几是多少”的问题解答。
一般单位要统一，注意比的前后要一致，就是等号两边都是图上距离与实际距离的比，或者是反过来，再就是注意大的比大的，等于小的比小的。
根据各部分的比，确定各部分与总量之间的关系，即各部分占总量的几分之几，然后按照“求一个数（这里指分配的量）的几分之几是多少”的问题解答。
一般单位要统一，注意比的前后要一致，就是等号两边都是图上距离与实际距离的比，或者是反过来，再就是注意大的比大的，等于小的比小的。
圆柱的体积公式：
v:体积 h:高 s:底面积 r:底面半径 c:底面周长
(1)侧面积=底面周长×高
(2)表面积=侧面积+底面积×2
(3)体积=底面积×高（即v=sh)
(4)底面积=半径×半径×3.14
圆柱的体积=底面积×高即：v=sh=πr2h。
圆锥的体积公式：
S侧=πrl=（nπl2）/360（r：底面半径，l：母线长，n：圆心角度数）
底面周长（C）=2πr=（nπl）/180（r：底面半径，n：圆心角度数，l：母线长）
h=根号（l2-r2）（l：母线长，r：底面半径）
全面积（S）=S侧+S底
V=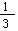
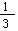Sh=πr·2h（S：底面积，r：底面半径，h：高）
V（圆锥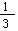）=·V（圆柱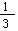）=·Sh =1/3·πr2h（S：底面积，r：底面半径，h：高）
S侧=πrl=（nπl2）/360（r：底面半径，l：母线长，n：圆心角度数）
底面周长（C）=2πr=（nπl）/180（r：底面半径，n：圆心角度数，l：母线长）
h=根号（l2-r2）（l：母线长，r：底面半径）
全面积（S）=S侧+S底
V=
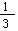Sh=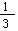πr·2h（S：底面积，r：底面半径，h：高）V（圆锥）=
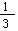·V（圆柱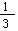）=·Sh =1/3·πr2h（S：底面积，r：底面半径，h：高） 发现相似题
与“一个圆柱和一个圆锥高相等，它们底面积的比是3：1，它们体积...”考查相似的试题有：
- 有两个圆，它们的面积之差为209平方厘米，已知大圆周长与小圆周长的比为10：9，问小圆的面积是多少？
- 求下列圆柱体的表面积：（1）底面半径是4厘米，高是6厘米．（2）底面直径是6厘米，高是12厘米．（3）底面周长是25.12厘米，高...
- 如图1所示，一瓶易拉罐底面直径是6厘米，高10厘米．（1）这瓶易拉罐能装饮料多少毫升？（2）王叔叔买来一箱这样的饮料，如图2...
- 用长6.28分米，宽3.14分米的纸板，可围成容积约是9.9立方分米的圆柱体状纸筒．______．
- 一个圆柱与一个圆锥的体积相等，它们的底面积的比是3：1，高的比是[ ]A．1：3B．3：1C．9：1D．1：9
- 一个圆柱的底面半径是6厘米，高是2分米，求这个圆柱的体积．
- 圆锥形沙堆，底面半径2米，高3米，它的占地面积是______平方米，体积______立方米．
- 计算圆锥的体积．（单位：厘米）
- 工地上有一些沙子，堆起来近似于一个圆锥，这堆沙子大约多少立方米？如果把这些沙子铺在宽3米，厚8厘米的路面上，可以铺多长...
- 一个圆锥的底面半径是2分米，高3分米，这个圆锥的体积是（ ）。