返回

高中三年级数学

首页
首页 高中三年级数学知识 点到直线的距离 圆的参数方程 椭圆的参数方程 直线的参数方程 试题正文
  • 解答题
    （选做题）
    已知曲线C1：（t为参数），C2：（θ为参数）。
    （1）化C1，C2的方程为普通方程
    （2）若C1上的点P对应的参数为，Q为C2上的动点，求PQ中点M到直线C3：（t为参数）距离的最小值
    本题信息：2012年黑龙江省模拟题数学解答题难度较难 来源:沈诺（高中数学）
  • 本题答案
    查看答案
本试题 “（选做题）已知曲线C1：（t为参数），C2：（θ为参数）。（1）化C1，C2的方程为普通方程（2）若C1上的点P对应的参数为，Q为C2上的动点，求PQ中点M到直线C3：（...” 主要考查您对

点到直线的距离

圆的参数方程

椭圆的参数方程

直线的参数方程

等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
  • 点到直线的距离
  • 圆的参数方程
  • 椭圆的参数方程
  • 直线的参数方程

点到直线的距离公式：

1、若点P（x0，y0）在直线Ax+By+C=0（A，B不同时为0）上，则Ax0+By0+C=0。
2、若点P（x0，y0）不在直线Ax+By+C=0（A，B不同时为0）上，则Ax0+By0+C≠0，此时点P（x0，y0）直线Ax+By+C=0（A，B不同时为0）的距离d=。


点到直线的距离公式的理解：

①点到直线的距离是直线上的点与直线外一点的连线的最短距离（这是从运动观点来看的）．
②若给出的直线方程不是一般式，则应先把方程化为一般式，再利用公式求距离．
③点到直线的距离公式适用于任何情况，其中点P在直线l上时，它到直线的距离为0．
④点到几种特殊直线的距离：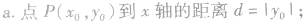
 

 

 
 

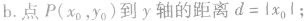
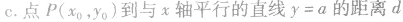
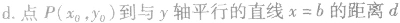
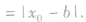
圆的参数方程：

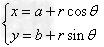（θ∈[0，2π）），（a，b）为圆心坐标，r为圆的半径，θ为参数（x，y）为经过点的坐标。

 


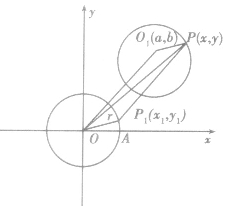
圆心为原点，半径为r的圆的参数方程：

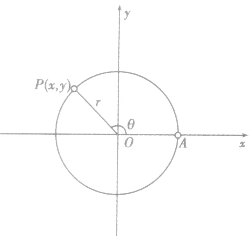
如图，如果点P的坐标为(x，y)，圆半径为r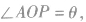， 根据三角函数定义，点P的横坐标x、纵坐标y都是θ的函数，即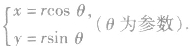
 


椭圆的参数方程：

椭圆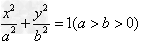的参数方程是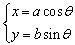，θ∈[0，2π）。


椭圆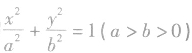的参数方程的理解：

如图，以原点为圆心，分别以a，b（a>b>0）为半径作两个圆，点B是大圆半径OA与小圆的交点，过点A作AN⊥Ox，垂足为N，过点B作BM⊥AN，垂足为M，求当半径OA绕点O旋转时，点M的横坐标与点A的横坐标相同，点M的纵坐标与点B的纵坐标相同．而A、B的坐标可以通过引进参数建立联系．设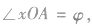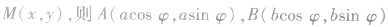，由已知得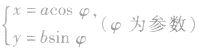，即为点M的轨迹参数方程，消去参数得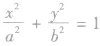，即为点M的轨迹普通方程。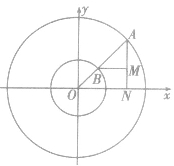
(1)参数方程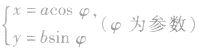，是椭圆的参数方程；
(2)在椭圆的参数方程中，常数a、b分别是椭圆的长半轴长和短半轴长．a>b,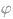称为离心角，规定参数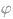的取值范围是[0，2π）;
(3)焦点在y轴的参数方程为


直线的参数方程：

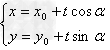过定点倾斜角为α的直线的参数方程为（t为参数）。


直线的参数方程及其推导过程：

设e是与直线l平行且方向向上(l的倾斜角不为0)或向右（l的倾斜角为0）的单位方向向量（单位长度与坐标轴的单位长度相同）．直线l的倾斜角为α，定点M0、动点M的坐标分别为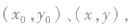
 

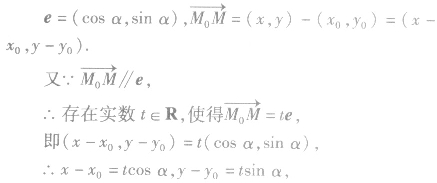
直线的参数方程中参数t的几何意义是：表示参数t对应的点M到定点Mo的距离，当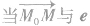同向时，t取正数；当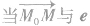异向时，t取负数；当点M与Mo重合时，t=0．


发现相似题
与“（选做题）已知曲线C1：（t为参数），C2：（θ为参数）。（1）...”考查相似的试题有：