相反数的定义：
像2和-2，5和-5这样，只有符号不同的两个数叫做互为相反数。
相反数的几何意义：在数轴上到原点距离相等的两个点表示的两个数叫做互为相反数。
相反数的代数意义：如果两个数的和为零，其中一个数是另一个数的相反数，这两个数称为互为相反数。

相反数的特性：
1、若a，b互为相反数，则a+b=0; 反之,若a+b=0，则a,b互为相反数；
2、在数轴上，互为相反数（0除外）的两个点位于原点的两旁，并且关于原点对称；
3、此时，b的相反数为﹣b=﹣(﹣a)=a，那么我们就说“相反数具有互称性”。
4、相反数的规律：正数的相反数是负数，负数的相反数是正数，0的相反数是0。
5、相反数的表示方法：a的相反数是-a，-a的相反数是a；a-b的相反数是b-a，b-a的相反数是a-b；a+b的相反数是-（a+b），即-a-b。

 

(互为)相反数的代数意义：
1、只有符号不同的两个数称互为相反数。a和-a是一对互为相反数，a叫做-a的相反数，-a叫做a的相反数。注意：-a不一定是负数。a不一定是正数。（a不等于0）
2、若两个实数a和b满足b=﹣a。我们就说b是a的相反数。
3、两个互为相反数的实数a和b必满足a+b=0。也可以说实数a和b满足a+b=0，则这两个实数a,b互为相反数。

相反数的判别：
我们在利用相反数的概念进行化简时，很多情况下，把括号里的部分看成一个整体（即想象成一个数a），问题就容易解决。因此要求一个数的相反数，只要在这个数前面叫上“-”，再化简即可。

多重符号的化简：
1、在一个数前面添加一个“+”好，所得的数与原数相同。
2、在一个数前面添加一个“-”号，所得的数就成为原数的相反数。
3、对于有三个火三个以上符号的数的化简，首先要注意，一个数前面不管有多少个“+”号，可以把正号去掉，其次要看“-”号的个数，当“-”号的个数为偶数个时，结果取正，当“-”号的个数为奇数个时，结果取“-”号。

绝对值定义：
在数轴上，表示一个数的点到原点的距离叫做这个数的绝对值。
绝对值用“||”来表示。
在数轴上，表示一个数a的点到数b的点之间的距离的值，叫做a-b的绝对值，记作|a-b|。
绝对值的意义：
1、几何的意义：
在数轴上，一个数到原点的距离叫做该数的绝对值．如：5指在数轴上表示数5的点与原点的距离，这个距离是5，所以5的绝对值是5。

2、代数的意义：
非负数（正数和0,）
非负数的绝对值是它本身，非正数的绝对值是它的相反数。
互为相反数的两个数的绝对值相等。
a的绝对值用“|a |”表示．读作“a的绝对值”。
实数a的绝对值永远是非负数，即|a |≥0。
互为相反数的两个数的绝对值相等，即|-a|=|a|。
若a为正数，则满足|x|=a的x有两个值±a，如|x|=3，,则x=±3.

绝对值的有关性质：
①任何有理数的绝对值都是大于或等于0的数，这是绝对值的非负性；
②绝对值等于0的数只有一个，就是0；
③绝对值等于同一个正数的数有两个，这两个数互为相反数；
④互为相反数的两个数的绝对值相等。

绝对值的化简：
绝对值意思是值一定为正值，按照“符号相同为正，符号相异为负”的原则来去绝对值符号。
①绝对值符号里面为负，在去掉绝对值时必须要加一个负的符号老确保整个值为正值，也就是当：
│a│=a (a为正值，即a≥0 时）；│a│=-a （a为负值，即a≤0 时）
②整数就找到这两个数的相同因数；
③小数就把这两个数同时扩大相同倍数成为整数,一般都是扩大10、100倍；
④分数的话就相除，得数是分数就是分子：分母，要是得数是整数，就这个数比1。

倒数的定义：
如果两个数的乘积等于1，那么这两个数就叫做互为倒数。
倒数性质：
（1）若a、b互为倒数，则ab=1，或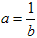，反之也成立；
（2）0没有倒数；
（3）乘积为-1的两个数互为负倒数，即ab=-1，则ab互为负倒数，反之也成立。

倒数的特点：
一个正实数（1除外）加上它的倒数 一定大于2。
理由：a/b,b/a为倒数当a>b时a/b一定大于1，可写为1+(a-b)/b。因为：
   b/a+(a-b)/a
=b×b/a×b+(a÷b-b×b)/ab
=(a×a-b×b+b×b)/ab
=a×a/a×b，
又因为a>b，
所以a·a>a·b，
所以a·a/a·b>1，
所以1+(a-b)/b+a·a/a·b>2，
所以一个正实数加上它的倒数一定大于2。
当b>a时也一样。
同理可证，一个负实数（-1除外）加上它的倒数一定小于-2。
倒数的求法：
1.求一个分数的倒数，例如3/4，我们只须把3/4这个分数的分子和分母交换位置，即得3/4的倒数为4/3。

2.求一个整数的倒数，只须把这个整数看成是分母为1的分数，然后再按求分数倒数的方法即可得到。
如12，即12/1，再把12/1这个分数的分子和分母交换位置，把分子做分母，分母做分子，则有1/12。　即12倒数是1/12。
说明:倒数是本身的数是1和-1。（0没有倒数）

把0.25化成分数，即1/4
再把1/4这个分数的分子和分母交换位置，把原来的分子做分母，原来的分母做分子.则是4/1
再把4/1化成整数，即4
所以0.25是4的倒数。也可以说4是0.25的倒数
也可以用1去除以这个数，例如0.25
1/0.25等于4
所以0.25的倒数4.
因为乘积是1的两个数互为倒数。
分数、整数也都使不完整用这种规律。