本试题 “已知两圆的半径恰为方程2x2-5x+2=0的两根,圆心距为23,则这两个圆的外公切线有( )A.0条B.1条C.2条D.3条” 主要考查您对一元二次方程根与系数的关系
圆和圆的位置关系(圆和圆的相离,圆与圆的相交,圆与圆的相切)
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 一元二次方程根与系数的关系
- 圆和圆的位置关系(圆和圆的相离,圆与圆的相交,圆与圆的相切)
一元二次方程根与系数的关系:
如果方程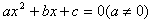 的两个实数根是
的两个实数根是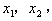 那么
那么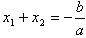 ,
,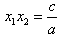 。
。
也就是说,对于任何一个有实数根的一元二次方程,两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商。
如果方程
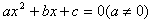 的两个实数根是
的两个实数根是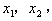 那么
那么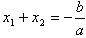 ,
,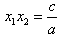 。
。也就是说,对于任何一个有实数根的一元二次方程,两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商。
一元二次方程根与系数关系的推论:
1.如果方程x2+px+q=0的两个根是x1、x2,那么x1+x2=-p , x1`x2=q
2.以两个数x1、x2为根的一元二次方程(二次项系数为1)是x2-(x1+x2)x+x1x2=0
提示:
①运用根与系数的关系和运用根的判别式一样,都必须先把方程化为一般形式,以便正确确定a、b、c的值。
②有推论1可知,对于二次项系数为1的一元二次方程,他的两根之和等于一次项系数的相反数,两根之积等于常数项。
③推论2可以看作推论1的逆定理,利用推论2可以直接求出以两个数x1、x2为根的一元二次方程(二次项系数是1)是x2-(x1+x2)x+x1x2=0
圆和圆的位置关系:
如果两个圆没有公共点,那么就说这两个圆相离,相离分为外离和内含两种。
如果两个圆只有一个公共点,那么就说这两个圆相切,相切分为外切和内切两种。
如果两个圆有两个公共点,那么就说这两个圆相交。
圆心距:两圆圆心的距离叫做两圆的圆心距。
如果两个圆没有公共点,那么就说这两个圆相离,相离分为外离和内含两种。
如果两个圆只有一个公共点,那么就说这两个圆相切,相切分为外切和内切两种。
如果两个圆有两个公共点,那么就说这两个圆相交。
圆心距:两圆圆心的距离叫做两圆的圆心距。
圆和圆位置关系的性质与判定:
设两圆的半径分别为R和r,圆心距为d,那么
两圆外离 d>R+r(没有交点)
d>R+r(没有交点)
两圆外切 d=R+r (有一个交点,叫切点)
d=R+r (有一个交点,叫切点)
两圆相交 R-r<d<R+r(R≥r)(有两个交点)
R-r<d<R+r(R≥r)(有两个交点)
两圆内切 d=R-r(R>r) (有一个交点,叫切点)
d=R-r(R>r) (有一个交点,叫切点)
两圆内含 d<R-r(R>r)(没有交点)
d<R-r(R>r)(没有交点)
两圆相切的性质:
(1)连心线:两圆圆心的连线。
(2)两圆相切的性质:相切两圆的连心线必过切点,即两圆圆心、切点三点在一条直线上。
发现相似题
与“已知两圆的半径恰为方程2x2-5x+2=0的两根,圆心距为23,则这...”考查相似的试题有:
- 已知关于x的方程x2+mx-6=0的一个根为2,则m=______,另一个根是______.
- 若关于x的方程2x2+kx﹣6=0的一个根为﹣3,则k=( ),另一根为( )。
- 我们知道当b2-4ac≥0,ax2+bx+c=0(a≠0)的根设x1,x2是方程的两个根,则x1+x2=_________,x1x2=_________当b2-4ac=0时,x1___...
- 如果a、b是一元二次方程x2-x-3=0的两个根,那么a3b-a2b的值为( )A.-6B.6C.-9D.9
- 已知关于x的二次方程a2x2+2ax+1=-3x的两个实数根的积为1,且关于x的二次方程x2+2(a+n)x-a2=4-6a-2n有小于2的正实根,求n的...
- 当a取什么值时,一元二次方程ax2+4x-1=0。(1)方程有两个相等的实数根;(2)方程有两个不相等的实数根。
- 已知一元二次方程x2+px+q+1=0的一根为2。(1)求q关于p的关系式;(2)求证:抛物线y=x2+px+q与x轴有两个交点;(3)设抛物线...
- 方程x2-4x+3=0的两根之积为( )A.4B.-4C.3D.-3
- 已知⊙O与⊙O′外切于点C,它们的半径分别为R,r,AB为两圆外公切线,切点为A,B,则公切线的长AB等于( )A.4RrB.RrC.2RrD.2Rr
- 已知⊙O1的半径为3cm,⊙O2的半径为7cm,若⊙O1和⊙O2的公共点不超过1个,则两圆的圆心距不可能为( ) A.0 cm B.4 cm C.8 cm ...