椭圆的离心率:
椭圆的焦距与长轴长之比叫做椭圆的离心率。
椭圆的性质:
1、顶点:A(a,0),B(-a,0),C(0,b)和D(0,-b)。
2、轴:对称轴:x轴,y轴;长轴长|AB|=2a,短轴长|CD|=2b,a为长半轴长,b为短半轴长。
3、焦点:F1(-c,0),F2(c,0)。
4、焦距: 。
。
5、离心率: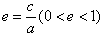 ;
;
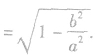
离心率对椭圆形状的影响:e越接近1,c就越接近a,从而b就越小,椭圆就越扁;e越接近0,c就越接近0,从而b就越大,椭圆就越圆;
6、椭圆的范围和对称性: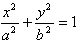 (a>b>0)中-a≤x≤a,-b≤y≤b,对称中心是原点,对称轴是坐标轴。
(a>b>0)中-a≤x≤a,-b≤y≤b,对称中心是原点,对称轴是坐标轴。
 。
。
利用椭圆的几何性质解题:
利用椭圆的几何性质可以求离心率 及椭圆的标准方程.要熟练掌握将椭圆中的某些线段长用a,b,c表示出来,例如焦点与各顶点所连线段的长,过焦点与长轴垂直的弦长等,这将有利于提高解题能力。
及椭圆的标准方程.要熟练掌握将椭圆中的某些线段长用a,b,c表示出来,例如焦点与各顶点所连线段的长,过焦点与长轴垂直的弦长等,这将有利于提高解题能力。
椭圆中求最值的方法:
求最值有两种方法:
(1)利用函数最值的探求方法利用函数最值的探求方法,将其转化为函数的最值问题来处理.此时应充分注意椭圆中x,y的范围,常常是化为闭区间上的二次函数的最值来求解。
(2)数形结合的方法求最值解决解析几何问题要注意数学式子的几何意义,寻找图形中的几何元素、几何量之间的关系.
椭圆中离心率的求法:
在求离心率时关键是从题目条件中找到关于a,b,c的两个方程或从题目中得到的图形中找到a,b,c的关系式,从而求离心率或离心率的取值范围.
双曲线的离心率的定义:
(1)定义:双曲线的焦距与实轴长的比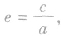 叫做双曲线的离心率.
叫做双曲线的离心率.
(2)e的范围:e>l.
(3)e的含义:e是表示双曲线开口大小的一个量,e越大开口越大.
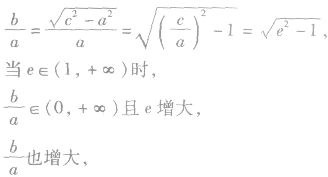
渐近线与实轴的夹角也增大。
双曲线的性质:
1、焦点在x轴上:顶点:(a,0),(-a,0);焦点:(c,0),(-c,0);
渐近线方程: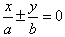 或
或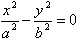 。
。
2、焦点在y轴上:顶点:(0,-a),(0,a);焦点:(0,c),(0,-c);
渐近线方程: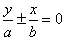 或
或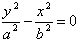 。
。
3、轴:x、y为对称轴,实轴长为2a,虚轴长为2b,焦距2c。
4、离心率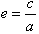 ;
;
5、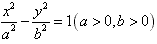 中,取值范围:x≤-a或x≥a,y∈R,对称轴是坐标轴,对称中心是原点。
中,取值范围:x≤-a或x≥a,y∈R,对称轴是坐标轴,对称中心是原点。
双曲线的焦半径:
双曲线上的点 之间的线段长度称作焦半径,分别记作
之间的线段长度称作焦半径,分别记作

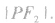
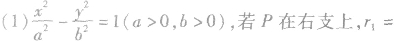
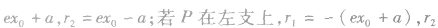
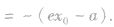
关于双曲线的几个重要结论:
(1)弦长公式(与椭圆弦长公式相同).
(2)焦点三角形:已知

的两个焦点,P为双曲线上一点(异于顶点),

的面积为
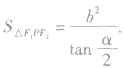
在解决与焦点三角形有关的问题时,应注意双曲线的两个定义、焦半径公式以及三角形的边角关系、正弦定理等知识的综合运用,还应注意灵活地运用平面几何、三角函数等知识来分析解决问题.
(3)基础三角形:如图所示,△AOB中,
(4)双曲线的一个焦点到一条渐近线的距离等于虚半轴长.
(5)自双曲线的焦点作渐近线的垂线,垂足必在相应的准线上,即过焦点所作的渐近线的垂线,渐近线及相应准线三线共点.
(6)以双曲线的焦半径为直径的圆与以实轴为直径的圆外切或内切.
(7)双曲线
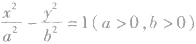
上一点P(x
0,y
0)处的切线方程是

(8)双曲线划分平面区域:对于双曲线
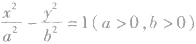
,我们有:P(x
0,y
0)在双曲线内部(与焦点共区域)
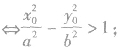
P(x
0,y
0)在双曲线外部(与焦点不其区域)
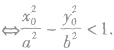
抛物线的性质(见下表):

抛物线的焦点弦的性质:
关于抛物线的几个重要结论:
(1)弦长公式同椭圆.
(2)对于抛物线y2=2px(p>0),我们有P(x0,y0)在抛物线内部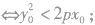 P(x0,y0)在抛物线外部
P(x0,y0)在抛物线外部
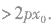
(3)抛物线y2=2px上的点P(x1,y1)的切线方程是 抛物线y2=2px(p>0)的斜率为k的切线方程是y=kx+
抛物线y2=2px(p>0)的斜率为k的切线方程是y=kx+
(4)抛物线y2=2px外一点P(x0,y0)的切点弦方程是
(5)过抛物线y2=2px上两点
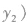 的两条切线交于点M(x0,y0),则
的两条切线交于点M(x0,y0),则
(6)自抛物线外一点P作两条切线,切点为A,B,若焦点为F,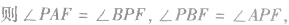 又若切线PA⊥PB,则AB必过抛物线焦点F.
又若切线PA⊥PB,则AB必过抛物线焦点F.
利用抛物线的几何性质解题的方法:
根据抛物线定义得出抛物线一个非常重要的几何性质:抛物线上的点到焦点的距离等于到准线的距离.利用抛物线的几何性质,可以进行求值、图形的判断及有关证明.
抛物线中定点问题的解决方法:
在高考中一般以填空题或选择题的形式考查抛物线的定义、标准方程以及几何性质等基础知识,在解答题中常常将解析几何中的方法、技巧与思想集于一身,与其他圆锥曲线或其他章节的内容相结合,考查综合分析问题的能力,而与抛物线有关的定值及最值问题是一个很好的切人点,充分利用点在抛物线上及抛物线方程的特点是解决此类题型的关键,在求最值时经常运用基本不等式、判别式以及转化为函数最值等方法。
利用焦点弦求值:
利用抛物线及焦半径的定义,结合焦点弦的表示,进行有关的计算或求值。
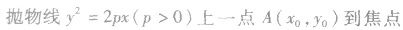
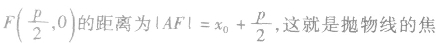
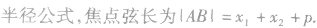
抛物线中的几何证明方法:
利用抛物线的定义及几何性质、焦点弦等进行有关的几何证明是抛物线中的一种常见题型,证明时注意利用好图形,并做好转化代换。