返回

高中数学

首页
首页 高中数学知识 一元高次（二次以上）不等式 基本不等式及其应用 试题正文
  • 解答题
    已知x，y∈R．
    （I）若x＞0，y＞0且
    1
    x
    +
    4
    y
    =1    ，求x+y的最小值；
    （II）若f(x)=
    1，x≥0
    -1，x＜0
    ，求不等式x+（x+2）•f（x+2）≤5的解集．
    本题信息：数学解答题难度较难 来源:未知
  • 本题答案
    查看答案
本试题 “已知x，y∈R．（I）若x＞0，y＞0且1x+4y=1，求x+y的最小值；（II）若f(x)=1，x≥0-1，x＜0，求不等式x+（x+2）•f（x+2）≤5的解集．” 主要考查您对

一元高次（二次以上）不等式

基本不等式及其应用

等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
  • 一元高次（二次以上）不等式
  • 基本不等式及其应用

元高次不等式的概念：

含有一个未知数且未知数的最高次数不小于3的不等式叫做一元高次不等式


一元高次不等式的解法：

①解一元高次不等式时，通常需进行因式分解，化为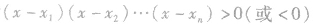的形式，然后应用区间法化为不等式组或用数轴标根法求解集．
②用数轴标根法求解一元高次不等式的步骤如下：
a．化简：将原不等式化为和它同解的基本型不等式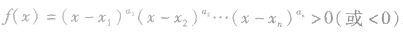．其中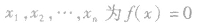的n个根，它们两两不等，通常情况下，常以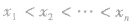的形式出现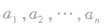， 为相同因式的幂指数，它们均为自然数，可以相等；
b．标根：将标在数轴上，将数轴分成(n+1)个区间；
c．求解：若 ，则从最右边区间的右上方开始画一条连续的曲线，依次穿过每一个零点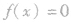（的根对应的数轴上的点），穿过最左边的零点后，曲线不再改变方向，向左下或左上的方向无限伸展．这样，不等式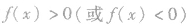的解集就直观、清楚地表示在图上，这种方法叫穿针引线法（或数轴标根法）；当 不全为l，即f（x）分解因式出现多重因式（即方程f(x）=0出现重根）时，对于奇次重因式对应的根，仍穿轴而过；对于偶次重因式对应的根，则应使曲线与轴相切．简言之，函数f(x)中有重因式时，曲线与轴的关系是"奇穿偶切"．


基本不等式：

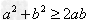（当且仅当a＝b时取“=”号）；
变式：①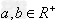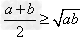，（当且仅当a＝b时取“=”号），即两个正数的算术平均不小于它们的几何平均。
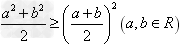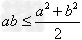②；③；④；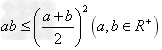


对基本不等式的理解：

(1)基本不等式的证明是利用重要不等式推导的，即，即有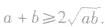
(2)基本不等式又称为均值定理、均值不等式等，其中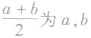的算术平均数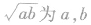，的几何平均数，本定理也可叙述为：两个正数的算术平均数不小于它们的几何平均数．
(3)要特别注意不等式成立的条件和等号成立的条件．均值不等式中：①当a=b时取等号，即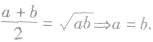


对于两个正数x，y，若已知xy，x+y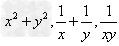，中的某一个为定值，可求出其余各个的最值：
如：（1）当xy＝P（定值），那么当x=y时，和x+y有最小值2，；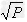
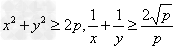（2）x+y=S（定值），那么当x=y时，积xy有最大值，；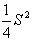
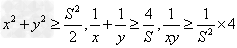（3）已知x2+y2=p，则x+y有最大值为，。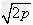

应用基本的不等式解题时：

注意创设一个应用基本不等式的情境及使等号成立的条件，即“一正、二定、三相等”。

利用基本不等式比较实数大小：

(1)注意均值不等式的前提条件．
(2)通过加减项的方法配凑成使用均值定理的形式．
(3)注意“1”的代换．
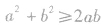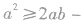
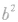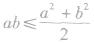(4)灵活变换基本不等式的形式，并注重其变形形式的运用．重要不等式的形式可以是，也可以是，还可以是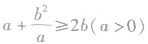等，不仅要掌握原来的形式，还要掌握它的几种变形形式以及公式的逆用等，以便应用．
(5)合理配组，反复应用均值不等式。 


基本不等式的几种变形公式：
 
 

发现相似题
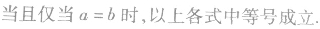
与“已知x，y∈R．（I）若x＞0，y＞0且1x+4y=1，求x+y的最小值；（...”考查相似的试题有：