本试题 “下图是某几何体的展开图.(1)这个几何体的名称是_________;(2)画出这个几何体的三视图;(3)求这个几何体的体积.(π取3.14)” 主要考查您对几何体的展开图
几何体的表面积,体积
尺规作图
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 几何体的展开图
- 几何体的表面积,体积
- 尺规作图
有些立体图形是由一些平面图形围成的,将它们的表面适当的剪开,可以展开成平面图形,这样的平面图形称为相应立体图形的展开图。
几何体展开图规律:
1.沿多面体的棱将多面体剪开成平面图形,若干个平面图形也可以围成一个多面体;
2.同一个多面体沿不同的棱剪开,得到的平面展开图是不一样的,就是说:同一个立体图形可以有多种不同的展开图。
注意:
①正方体展开头记忆口诀:
正方体盒巧展开,六个面儿七刀裁;
十四条边布周围,十一类图记分明;
四方成线两相卫,六种图形巧组合;
跃马失蹄四分开;两两错开一阶梯。
对面相隔不相连,识图巧排“7”、“凹”、“田”。
②在正方体的展开图中,一条直线上的小正方形不会超过四个。
③正方体的展开图不会有"田"字形,"凹"字形的形状。
图形展开图:
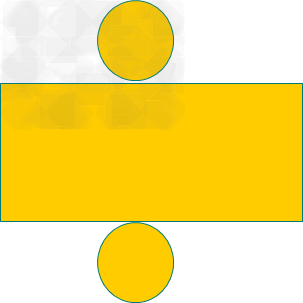
1.圆柱展开图:
 →→
→→
2.圆锥展开图:
 →→
→→
3.长方体展开图:
 →→
→→
4.正方体展开图:
 →→
→→
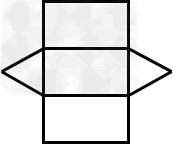
5.三棱柱展开图:
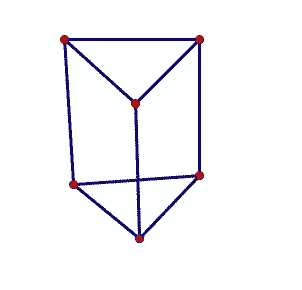 →→
→→
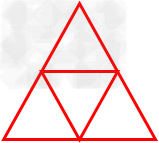
6.三棱锥展开图:
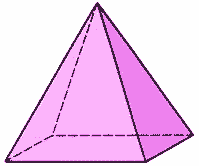 →→
→→
认识柱、锥、台、球及其简单组合体的结构特征,了解柱、锥、台、球的概念;
了解柱、锥、台、球的表面积与体积的计算,并能运用公式计算柱、锥、台、球及其简单组合体的表面积与体积。
几何体一般概念及性质:
1、圆柱:可以看做以矩形的一边为旋转轴、旋转一周形成的曲面所围成的几何体
2、圆锥:可以看做以直角三角形的一直角边为旋转轴、旋转一周形成的曲面所围成的几何体
3、圆台:可以看做以直角梯形中垂直于底边的腰所在的直线为旋转轴、旋转一周形成的曲面所围成的几何体
4、球:一个半圆绕着它的直径所在的直线旋转一周所形成的曲面所围成的几何体
5、棱柱有两个面互相平行、而其余每相邻两个面的交线都互相平行
6、多面体是由若干个平面多边形所围成的几何体
7、棱锥有一个面是多边形,而其余个面都是有一个公共顶点的三角形
几何体的表面积,体积计算公式:
1、圆柱体:
表面积:2πRr+2πRh
体积:πR2h (R为圆柱体上下底圆半径,h为圆柱体高)
2、圆锥体:
表面积:πR2+πR[(h2+R2)的平方根]
体积: πR2h/3 (r为圆锥体低圆半径,h为其高,
3、正方体:
a-边长,
S=6a2 ,V=a3
4、长方体:
a-长 ,b-宽 ,c-高
S=2(ab+ac+bc) V=abc
5、棱柱:
S-底面积 h-高
V=Sh
6、棱锥 :
S-底面积 h-高
V=Sh/3
7、棱台:
S1和S2-上、下底面积 h-高
V=h[S1+S2+(S1S2)^1/2]/3
8、拟柱体:
S1-上底面积 ,S2-下底面积 ,S0-中截面积 h-高,
V=h(S1+S2+4S0)/6
9、圆柱:
r-底半径 ,h-高 ,C—底面周长 S底—底面积 ,S侧—侧面积 ,S表—表面积
C=2πr S底=πr2,S侧=Ch ,S表=Ch+2S底 ,V=S底h=πr2h
10、空心圆柱:
R-外圆半径 ,r-内圆半径 h-高
V=πh(R^2-r^2)
11、直圆锥 :
r-底半径 h-高
V=πr^2h/3
12、圆台:
r-上底半径 ,R-下底半径 ,h-高
V=πh(R2+Rr+r2)/3
13、球:
r-半径 d-直径
V=4/3πr^3=πd^3/6
14、球缺
h-球缺高,r-球半径,a-球缺底半径
V=πh(3a2+h2)/6 =πh2(3r-h)/3
15、球台:
r1和r2-球台上、下底半径 h-高
V=πh[3(r12+r22)+h2]/6
16、圆环体:
R-环体半径 D-环体直径 r-环体截面半径 d-环体截面直径
V=2π2Rr2 =π2Dd2/4
17、桶状体:
D-桶腹直径 d-桶底直径 h-桶高
V=πh(2D2+d2)/12 ,(母线是圆弧形,圆心是桶的中心)
V=πh(2D2+Dd+3d2/4)/15 (母线是抛物线形)
是指限定用没有刻度的直尺和圆规来完成的画图。
一把没有刻度的直尺看似不能做什么,画一个圆又不知道它的半径,画线段又没有精确的长度。
其实尺规作图的用处很大,比如单用圆规找出一个圆的圆心,量度一个角的角度,等等。
运用尺规作图可以画出与某个角相等的角,十分方便。
尺规作图的中基本作图:
作一条线段等于已知线段;
作一个角等于已知角;
作线段的垂直平分线;
作已知角的角平分线;
过一点作已知直线的垂线。
还有:
已知一角、一边做等腰三角形
已知两角、一边做三角形
已知一角、两边做三角形
依据公理:
还可以根据已知条件作三角形,一般分为已知三边作三角形,已知两边及夹角作三角形,已知两角及夹边作三角形等,作图的依据是全等三角形的判定定理:SSS,SAS,ASA等。
注意:
保留全部的作图痕迹,包括基本作图的操作程序,只有保留作图痕迹,才能反映出作图的操作是否合理。
尺规作图方法:
任何尺规作图的步骤均可分解为以下五种方法:
·通过两个已知点可作一直线。
·已知圆心和半径可作一个圆。
·若两已知直线相交,可求其交点。
·若已知直线和一已知圆相交,可求其交点。
·若两已知圆相交,可求其交点。
尺规作图简史:
“规”就是圆规,是用来画圆的工具,在我国古代甲骨文中就有“规”这个字.“矩”就像现在木工使用的角尺,由长短两尺相交成直角而成,两者间用木杠连接以使其牢固,其中短尺叫勾,长尺叫股.
矩的使用是我国古代的一个发明,山东历城武梁祠石室造像中就有“伏羲氏手执矩,女娲氏手执规”之图形.矩不仅可以画直线、直角,加上刻度可以测量,还可以代替圆规.甲骨文中也有矩字,这可追溯到大禹治水(公元前2000年)前.
《史记》卷二记载大禹治水时“左准绳,右规矩”.赵爽注《周髀算经》中有“禹治洪水,……望山川之形,定高下之势,……乃勾股之所由生也.”意即禹治洪水,要先测量地势的高低,就必定要用勾股的道理.这也说明矩起源于很远的中国古代.
春秋时代也有不少著作涉及规矩的论述,《墨子》卷七中说“轮匠(制造车子的工匠)执其规矩,以度天下之方圆.”《孟子》卷四中说“离娄(传说中目力非常强的人)之明,公输子(即鲁班,传说木匠的祖师)之巧,不以规矩,不能成方圆.”可见,在春秋战国时期,规矩已被广泛地用于作图、制作器具了.由于我国古代的矩上已有刻度,因此使用范围较广,具有较大的实用性.
古代希腊人较重视规、矩在数学中训练思维和智力的作用,而忽视规矩的实用价值.因此,在作图中对规、矩的使用方法加以很多限制,提出了尺规作图问题.所谓尺规作图,就是只有限次地使用没有刻度的直尺和圆规进行作图.
古希腊的安那萨哥拉斯首先提出作图要有尺寸限制.他因政治上的纠葛,被关进监狱,并被判处死刑.在监狱里,他思考改圆成方以及其他有关问题,用来打发令人苦恼的无所事事的生活.他不可能有规范的作图工具,只能用一根绳子画圆,用随便找来的破木棍作直尺,当然这些尺子上不可能有刻度.另外,对他来说,时间是不多了,因此他很自然地想到要有限次地使用尺规解决问题.后来以理论形式具体明确这个规定的是欧几里德的《几何原本》.由于《几何原本》的巨大影响,希腊人所崇尚的尺规作图也一直被遵守并流传下来.
由于对尺规作图的限制,使得一些貌似简单的几何作图问题无法解决.最著名的是被称为几何三大问题的三个古希腊古典作图难题:立方倍积问题、三等分任意角问题和化圆为方问题.当时很多有名的希腊数学家,都曾着力于研究这三大问题,虽然借助于其他工具或曲线,这三大难题都可以解决,但由于尺规作图的限制,却一直未能如愿以偿.以后两千年来,无数数学家为之绞尽脑汁,都以失败而告终.直到1637年笛卡尔创立了解析几何,关于尺规作图的可能性问题才有了准则.到了1837年万芝尔首先证明立方倍积问题和三等分任意角问题都属于尺规作图不可能问题.1882年林德曼证明了π是无理数,化圆为方问题不可能用尺规作图解决,这才结束了历时两千年的数学难题公案.
与“下图是某几何体的展开图.(1)这个几何体的名称是_________...”考查相似的试题有:
- 已知圆柱的底面半径长和母线长是方程4x2-11x+2=0的两个根,则该圆柱的侧面展开图的面积是______.
- 如图,若要把一个正方体纸盒沿棱剪开,平铺在桌面上,则至少需要剪开的棱的条数是( ).A.5条B.6条C.7条D.8条
- 如图,折叠围成一个正方体时,数字( )会在与数字2所在的平面相对的平面上.
- 挂历纸长80cm,宽50cm,如图,请你利用挂历纸和事先准备好的透明胶布做成一个无盖的长方体纸盒(粘贴处既不重叠,又不能有空...
- 在下列方格纸中(1)过A点作PQ的垂线.(2)过A点作PQ的平行线.(3)点A到PQ的距离是______.
- 已知:如图,中,,绕点A旋转,旋转后,B 、C两点分别记作,并且,你能用学过的数学知识解决绕点A转过的角是多少度吗?
- 如图,在中,把△ABC绕AB边上的点D顺时针旋转90°得到△,交AB于点E,若AD=BE,则△的面积为
- 如图所示,A,B,C表示三个村庄,它们被三条河隔开,现在打算在每两个村庄之间修一条笔直的公路,则一共需要架多少座桥?请在...
- 已知线段a,b和∠α,用直尺和圆规作△ABC,使BC=a,AC=b,∠C=12∠α.(不写作法,保留作图痕迹)
- 如果一个点能与另外两个点能构成直角三角形,则称这个点为另外两个点的勾股点,例如:矩形ABCD中,点C与A,B两点可构成直角三...