本试题 “如图所示,气缸放置在水平台上,活塞质量为5 kg,面积为25 cm2,厚度不计,气缸全长25 cm,大气压强为1×105Pa,当温度为27℃时,活塞封闭的气柱长10 cm,若保...” 主要考查您对热力学第一定律
玻意耳定律(等温定律)
盖—吕萨克定律(等压定律)
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 热力学第一定律
- 玻意耳定律(等温定律)
- 盖—吕萨克定律(等压定律)
1、内容:物体内能的增量(ΔU)等于外界对物体做的功(W)和物体吸收的热量(Q)的总和。
2、表达式:W+Q=ΔU。
3、符号法则:外界对物体做功,W取正值,物体对外界做功,W取负值;物体吸收热量,Q取正值,物体放出热量,Q取负值;物体内能增加,ΔU取正值,物体内能减少,ΔU取负值。
热力学第一定律在理想气体中的应用方法:
1.功W的正负分析
若体积V增大,则W取“-”;若体积V减小,则形取“+”。
注意,若气体向真空中自由膨胀时,则W=0。
2.△U的正负分析
一定质量理想气体的内能只与温度有关。
若温度T增大,△U取“+”;若温度T减小,△U取“-”;若T不变,贝△U=0。
3.Q的正负分析:
绝热Q=0,吸热Q取“+”,放热Q取“-”。
4.气体状态变化还应结合 分析
分析
5.由图像讨论气体的功、热量和内能
(1)等温线(如图所示):一定质量的理想气体,
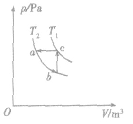
 ,等温降压膨胀,内能不变,吸热等于对外做的功。
,等温降压膨胀,内能不变,吸热等于对外做的功。 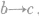 ,等容升温升压,不做功,吸热等于内能增加。
,等容升温升压,不做功,吸热等于内能增加。  ,等压降温压缩,放热等于外界做功和内能减少量。
,等压降温压缩,放热等于外界做功和内能减少量。
(2)等容线(如图所示):一定质量的理想气体, 。
。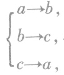 状态及能量变化同等温线分析。
状态及能量变化同等温线分析。
(3)等压线(如图所示):一定质量的理想气体.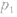
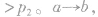 等温升压压缩,内能不变,外界做功等于放热;
等温升压压缩,内能不变,外界做功等于放热;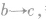 等压升温膨胀,吸热等于内能增加量和对外做的功;
等压升温膨胀,吸热等于内能增加量和对外做的功;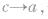 等容降温降压,内能减小量等于放热。
等容降温降压,内能减小量等于放热。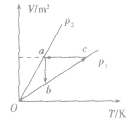
玻意耳定律:
1.概念:一定质量的某种气体,在温度不变的条件下其压强与体积变化时的关系,叫做气体的等温变化
2.规律:一定质量的气体,在温度不变的情况下,它的压强跟体积成反比—— 玻意耳定律3.公式: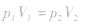
4.图像: 
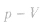 图线为双曲线,同一气体的两条等温线比较,双曲线顶点离坐标原点远的温度高,即
图线为双曲线,同一气体的两条等温线比较,双曲线顶点离坐标原点远的温度高,即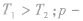
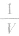 图线为过原点的直线,同一气体比较,斜率(
图线为过原点的直线,同一气体比较,斜率(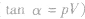 )大的温度高,即
)大的温度高,即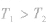 。
。
5.条件:m一定,p不太大,T不太低
6.微观解释:一定质量的理想气体,分子的总数是一定的,在温度保持不变时,分子的平均动能保持不变,气体的体积减小到原来的几分之一,气体的密度就增大到原来的几倍,因此压强就增大到原来的几倍,反之亦然,所以气体的压强与体积成反比。
液柱移动问题的求解方法:
液柱移动问题的分析方法
(1)假设推理法:根据题设条件,假设发生某种特殊的物理现象或物理过程,运用相应的物理规律及有关知识进行严谨的推理,得出正确的答案。巧用假设推理法可以化繁为简,化难为易,简捷解题。
(2)温度不变情况下的液柱移动问题的特点是:在保持温度不变的情况下改变其他题设条件,从而引起封闭气体液柱的移动,或液面的升降,或气体体积的增减。解决这类问题通常假设液柱不移动,或液面不升降,或气体体积不变,然后从假设出发,运用玻意耳定律等有关知识进行推论,求得正确答案。
(3)用液柱或活塞隔开两部分气体,当气体温度变化时,液柱或活塞是否移动?如何移动? 此类问题的特点是:气体的状态参量p、V、T都发生了变化,直接判断液柱或活塞的移动方向比较困难,通常先进行气体状态的假设,然后应用查理定律可以简单地求解:其一般思路为:
①先假设液柱或活塞不发生移动,两部分气体均做等容变化:
②对两部分气体分别应用查理定律的分比形式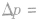
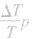 ,求出每部分气体压强的变化量△p,并加以比较。
,求出每部分气体压强的变化量△p,并加以比较。
a.如果液柱两端的横截面积相等,且△p均大于零,意味着两部分气体的压强均增大,则液柱向△p值较小的一方移动;若△p均小于零,意味着两部分气体的压强均减小,则液柱向压强减小量较大的一方(即|△p|较大的一方)移动;若△p相等,则液柱不移动。
b.如果液柱两端的横截面积不相等,则应考虑液柱两端的受力变化(△pS)。,若△p均大于零,则液往向△pS较小的一方移动;若△p均小于零,则液桂向|△pS|值较大的一方移动;若△p等于零,则液柱不移动。
盖-吕萨克定律:
1.概念:一定质量的某种气体,在压强不变时,体积随温度的变化叫做等压变化
2.规律一定质量的某种气体,在压强不变的情况下,其体积V与热力学温度T成正比——盖一吕萨克定律
3.公式: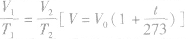
4.推论:
5.图像: 
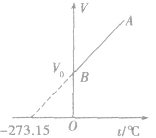
 图线是过原点的直线,压强越大,斜率越小,即
图线是过原点的直线,压强越大,斜率越小,即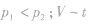 图线是过定点
图线是过定点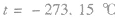 的直线,
的直线,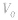 是
是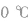 的体积。
的体积。
6.条件:m一定,p不太大,T不太低
7.微观解释:一定质量的理想气体,当温度升高时,气体分子的平均动能增大。要保持压强不变,必须减小单位体积内的分子个数,即增大气体的体积
封闭气体压强的求法:
有关气体压强的计算可转化为力学问题来处理。
1.参考液面法
(1)计算的主要依据是流体力学知识:
①液面下h深处由液体重力产生的压强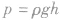 。 (注意:h是液柱竖直高度,不一定等于液柱的长度)
。 (注意:h是液柱竖直高度,不一定等于液柱的长度)
②若液面与外界大气相接触,则液面下h处的压强为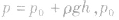 为外界大气压强。
为外界大气压强。
③帕斯卡定律(液体传递外加压强的规律):加在密闭静止液体上的压强,能够大小不变地由液体向各个方向传递。
④连通器原理:在连通器中,同一种液体(中间液体不间断)的同一水平上的压强是相等的。
(2)计算的方法步骤:选取一个假想的液体薄面 (其自重不计)为研究对象;分析液面两侧重力情况,建立力的平衡方程;消去横截面积,得到液面两侧的压强平衡方程;求得气体压强。 2.平衡法
欲求用固体(如活塞等)封闭在静止容器中的气体压强,应对固体(如活塞等)进行受力分析,然后根据力的平衡条件求解。
3.动力学法
当封闭气体所在的系统处于力学非平衡状态时,欲求封闭气体的压强,首先要恰当地选择对象(如与气体相关联的液柱、同体等),并对其进行正确的受力分析(特别注意分析内、外气体的压力),然后应用牛顿第二定律列方程求解。
与“如图所示,气缸放置在水平台上,活塞质量为5 kg,面积为25 cm...”考查相似的试题有:
- 气缸中的气体吸收了4×103J的热量,同时推动活塞对外做了1.8×103J的功,那么它的内能______(填“增加”或“减少”)了______J.
- 现代典型的燃煤发电厂,总效率一般为40%,有 一座大型燃煤发电厂,如果发出1.0 ×109J 的电能,可供一座大城市使用,下图表示...
- 有关热现象,以下说法正确的是( ) A.液体很难被压缩,是因为液体分子间无空隙 B.物体的内能增加,一定有外力对物体做功 C...
- 将一装有压缩空气的金属瓶的瓶塞突然打开,使压缩空气迅速跑出,当瓶内气体压强降至等于大气压p0时,立即盖紧瓶塞,过一段时...
- 下列说法正确的是[ ]A.布朗运动就是液体分子的热运动B.一定质量的理想气体在温度不变的条件下,压强增大,则外界对气体做功...
- 在下列叙述中,正确的是[ ]A.物体的温度越高,分子热运动越剧烈,分子平均动能越大B.布朗运动就是液体分子的热运动C.对一...
- (6分)如图甲,一个导热气缸竖直放置,气缸内封闭有一定质量的气体,活塞与气缸壁紧密接触,可沿汽缸壁无摩擦地上下移动。若...
- 大气压强对许多物理实验和化学实验有着重要影响。现用“验证玻意耳定律”的仪器来测量大气压强p0。注射器针筒已被固定在竖直方...
- 如图所示,某压缩式喷雾器储液桶的容量是5.7×10-3m3.往桶内倒入4.2×10-3m3的药液后开始打气,打气过程中药液不会向外喷...
- 【选修3-3选做题】一定质量的理想气体从状态A变化到状态B,再变化到状态C,其状态变化过程的p-V图象如图所示。已知该气体在状...