△ABC中，∠ACB=90°，AD是角平分线，CH是高，AD、CH交于点E，DF垂直于BC，垂足为F．求证：四边形CEFD是菱形．,初中,数学试题,菱形，菱形的性质，菱形的判定考点,角平分线的性质考点,好技网

解答题
△ABC中，∠ACB=90°，AD是角平分线，CH是高，AD、CH交于点E，DF垂直于BC，垂足为F．求证：四边形CEFD是菱形．

本题信息：数学解答题难度一般来源:未知
本题答案
查看答案

本试题 “△ABC中，∠ACB=90°，AD是角平分线，CH是高，AD、CH交于点E，DF垂直于BC，垂足为F．求证：四边形CEFD是菱形．” 主要考查您对
菱形，菱形的性质，菱形的判定

角平分线的性质
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。

菱形，菱形的性质，菱形的判定
角平分线的性质

菱形的定义:
在一个平面内，有一组邻边相等的平行四边形是菱形。

菱形的性质:
①菱形具有平行四边形的一切性质；
②菱形的对角线互相垂直且平分，并且每一条对角线平分一组对角；
③菱形的四条边都相等；
④菱形既是轴对称图形（两条对称轴分别是其两条对角线所在的直线），也是中心对称图形（对称中心是其重心，即两对角线的交点）；
⑤在有一个角是60°角的菱形中，较短的对角线等于边长，较长的对角线是较短的对角线的根号3倍。

菱形的判定:
在同一平面内，
（1）定义：有一组邻边相等的平行四边形是菱形
（2）定理1：四边都相等的四边形是菱形
（3）定理2：对角线互相垂直的平行四边形是菱形
菱形是在平行四边形的前提下定义的，首先它是平行四边形，而且是特殊的平行四边形，特殊之处就是“有一组邻边相等”，因而增加了一些特殊的性质和判定方法。
菱形的面积：S_菱形=底边长×高=两条对角线乘积的一半。

角平分线：
三角形的一个角的平分线与这个角的对边相交，连结这个角的顶点和与对边交点的线段叫做三角形的角平分线（也叫三角形的内角平分线）。由定义可知，三角形的角平分线是一条线段。由于三角形有三个内角，所以三角形有三条角平分线。三角形的角平分线交点一定在三角形内部。

角平方线定理：
①角平分线上的任意一点，到角两边的距离相等。垂直于两边为最短距离。
②角平分线能得到相同的两个角，都等于该角的一半。
③三角形三条角平分线相交于一点，并且这一点到三边的距离相等。
④三角形的三个角的角平分线相交于一点，这个点称为内心，即以此点为圆心可以在三角形内部画一个内切圆。
逆定理：
在角的内部，到角两边的距离相等的点在角平分线上。

角平分线作法：
在角AOB中，画角平分线

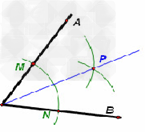
方法一：
1.以点O为圆心，以任意长为半径画弧，两弧交角AOB两边于点M，N。
2.分别以点M，N为圆心，以大于1/2MN的长度为半径画弧，两弧交于点P。
3.作射线OP。
则射线OP为角AOB的角平分线。
当然，角平分线的作法有很多种。下面再提供一种尺规作图的方法供参考。

方法二：
1.在两边OA、OB上分别截取OM、OA和ON、OB，且使得OM=ON，OA=OB；
2.连接AN与BM，他们相交于点P；
3.作射线OP。
则射线OP为角AOB的角平分线。

发现相似题

与“△ABC中，∠ACB=90°，AD是角平分线，CH是高，AD、CH交于点E，DF...”考查相似的试题有：