本试题 “已知点P(sinα•cosα,2cosα)在第四象限,则角α的终边在( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限” 主要考查您对象限角、轴线角
终边相同的角
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 象限角、轴线角
- 终边相同的角
象限角:
在直角坐标系中,使角的顶点与原点重合,角的始边与x轴的非负半轴重合,角的终边在第几象限,就说这个角是第几象限的角。
轴线角:
如果角的终边在坐标轴上,就认为这个角不属于任何象限,称为轴线角。
第一、二、三、四象限角的集合分别表示为:
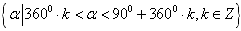 、
、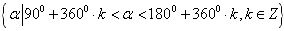 、
、 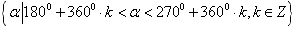 、
、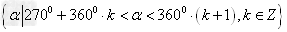 ;
;
轴线角的集合:
终边在x轴上的角的集合: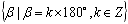 ;
;
终边在y轴上的角的集合: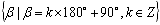 ;
;
终边在坐标轴上的角的集合: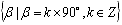 ;
;
已知α是第几象限的角,如何确定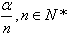 所在象限的角的常用方法:
所在象限的角的常用方法:
(1)分类讨论法,先根据α的范围用整数k把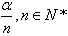 的范围表示出来,再对k分n种情况讨论;
的范围表示出来,再对k分n种情况讨论;
(2)几何法:把各象限均先n等分,再从x轴的正方向的上方起,依次将各区域标上①、②、③、④,则α原来是第几象限对应的标号即为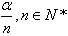 的终边所在的区域。
的终边所在的区域。
常用结论:
(1)已知α所在象限,求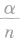
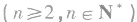 所在象限:通过分类讨论把角写成
所在象限:通过分类讨论把角写成 的形式,然后判断
的形式,然后判断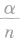 所在象限.
所在象限.
(2)由α所在象限,确定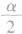 所在象限:
所在象限:
①画出区域:将坐标系每个象限二等分,得8个区域.
②标号:自x轴正向逆时针方向把每个区域依次标上I、Ⅱ、Ⅲ、Ⅳ,如图所示,
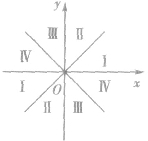
③确定区域:找出与角α所在象限标号一致的区域,即为所求.
(3)由α所在象限,确定 所在象限:
所在象限:
①画出区域:将坐标系每个象限三等分,得到12个区域.
②标号:自x轴正向逆时针方向把每个区域依次标上Ⅰ、Ⅱ、Ⅲ、Ⅳ,如图所示,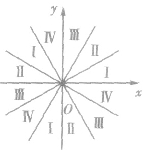
③确定区域:找出与角α所在象限标号一致的区域,即为所求.
终边相同的角的表示:
所有与角α终边相同的角,连同角α在内,可构成一个集合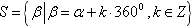 即任一与角α终边相同的角,都可以表示成角α与整数个周角的和。
即任一与角α终边相同的角,都可以表示成角α与整数个周角的和。
注:(1)k∈Z;
(2)α是任意角;
(3)k?360°与α之间是“+”;
(4)终边相同的角不一定相等,但相等的角的终边一定相同,终边相同的角有无数多个,它们的差是360°的整数倍。
举例说明:
举出画出与30°角的终边相同的一些角吗?390°角的终边、-330°角的终边。
390°=30°+360°
-330°=30°-360°
30°=30°+0×360°
1470°=30°+4×360°
-1770°=30°-5×360°
由特殊角30°看出:所有与30°角终边相同的角,连同30°角自身在内,都可以写成30°+
常见结论:
(1)角α为锐角,则α一定是第一象限的角,反之不一定成立。故角α是锐角是角α为第一象限角的充分不必要条件。
(2)角α为钝角,则α一定是第二象限的角,反之不一定成立。故角α是钝角是角α为第二象限角的充分不必要条件。
(3)第一象限的角不一定是正角。
与“已知点P(sinα•cosα,2cosα)在第四象限,则角α的终边在( )...”考查相似的试题有:
- 若α是第四象限角,且1-sinα=cosα2-sinα2,则α2是第______ 象限角.
- -1200°是第______象限角.
- 下列四个命题中,正确的是( ) A.第一象限的角必是锐角 B.锐角必是第一象限的角 C.终边相同的角必相等 D.第二象限的角必...
- 下列各角中,与30°的角终边相同的角是( ) A.60° B.120° C.-30° D.390°
- 与角-70°终边相同的角是( ) A.70° B.110° C.250° D.290°
- 下列各组角中,终边相同的角是( )A.k2π与kπ+π2(k∈Z)B.kπ±π3与k3π(k∈Z)C.(2k+1)π与(4k±1)π(k∈Z)D.kπ+π6与kπ±π...
- 与1000°终边相同的最小正角是 ______.
- 角α的终边经过点(-3,0),则角α是( ) A.第二象限角 B.第三象限角 C.第二或第三象限角 D.不是象限角
- 给出下列命题,其中正确的是( )(1)弧度角与实数之间建立了一一对应(2)终边相同的角必相等(3)锐角必是第一象限角(4)...
- 若角α,β的终边互为反向延长线,则α与β的关系一定是( ) A.α=-β B.α-β=-k•360°(k∈Z) C.α=180°+β D.α=(2k+1)180°+β(...