本试题 “求出下面各比的比值,并找出比值相等的比组成比例。2:12:0.4:8:2” 主要考查您对求比值
比例的意义,比例的基本性质
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 求比值
- 比例的意义,比例的基本性质
求比值:
用比的前项除以比的后项得到一个数,这个数就是比值。比值可以用分数表示,也可以用小数或整数表示。例如:
1:3的比值=1÷3=1/3;1/3也是一种写法,作比时读作一比三,做分数时读作三分之一。
两个比值相等的比可以组成比例,用"="号连接。例如:50:25=6:3
求比值方法:
求比值的目的是求一比的前项除以后项的结果。
①运用比的基本性质。如:
5/6:1/2=(5/6×6):(1/2×6)
比值为5/3
②运用比与除法的关系。如:
6.3:0.9=6.3÷0.9
比值为7;化简比为7∶1。
③运用比与分数的关系。如:
16:20=16/20=4/5
比值为4/5或0.8
用比的前项除以比的后项得到一个数,这个数就是比值。比值可以用分数表示,也可以用小数或整数表示。例如:
1:3的比值=1÷3=1/3;1/3也是一种写法,作比时读作一比三,做分数时读作三分之一。
两个比值相等的比可以组成比例,用"="号连接。例如:50:25=6:3
求比值方法:
求比值的目的是求一比的前项除以后项的结果。
①运用比的基本性质。如:
5/6:1/2=(5/6×6):(1/2×6)
比值为5/3
②运用比与除法的关系。如:
6.3:0.9=6.3÷0.9
比值为7;化简比为7∶1。
③运用比与分数的关系。如:
16:20=16/20=4/5
比值为4/5或0.8
表示两个比相等的式子叫做比例。
比例的基本性质:
组成比例的四个数,叫做比例的项。两端的两项叫做比例的外项,中间的两项叫做比例的内项。
在比例里,两个外项的积等于两个内项的积。
用字母表示为:如果  (a,b, c,d 都不等于零),那么ad=bc.
(a,b, c,d 都不等于零),那么ad=bc.
这是因为用bd去乘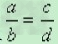 的两边,得
的两边,得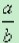 ?bd=
?bd= ?bd,所以ad=bc.
?bd,所以ad=bc.
性质推论:
从比例的这个基本性质,可以推得:
如果两个数的积等于另外两个数的积,那么这四个数可以组成比例。
用式子表示就是:如果ad=bc,那么 (b.d都不等于零)。
(b.d都不等于零)。
这是因为用bd 去除ad=bc两边,得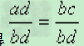 ,所以
,所以 。
。
比例意义:
正比例的意义:
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做成正比例关系。
正比例关系两种相关联的量的变化规律:同时扩大,同时缩小,比值不变。
反比例的意义:
成反比例的量包括三个数量,一个定量和两个变量。研究两个变量之间的扩大(或缩小)的变化关系。一种量发生变化,引起另一种量发生相反的变化。这两种量是反比例的量,它们的关系成反比例关系。
反比例实质:
两种相关联的量,一种量变化,另一种量也随着变化,这两种量中相对应的两个数的积一定。这两种量叫做成反比例的量。它们的关系叫做反比例关系。
发现相似题
与“求出下面各比的比值,并找出比值相等的比组成比例。2:12:0....”考查相似的试题有:
- 比的前项是9,后项是3,比值是[ ]A.B.3C.27
- 米:40厘米的比值是( ),化成最简单的整数比是( )。
- n=15m是根据下列( )项的比例式得到的.A.n:m=5:1B.m:5=1:nC.m:5=n:1
- 在下面的括号里填上合适的数,使它成为比例。36∶( )=54∶30.3∶0.5=6∶( )=6∶( )
- 因为A的3倍等于B的4倍,所以A:B=3:4.______.(判断对错)
- A×37=B×34,A、B均不为0,那么A:B=______:______.
- 现在、3、9三个数,再从下面选出一个就可以组成比例的数是[ ]A.6B.C.4D.
- 已知5x=8y,那么,y:x=______.
- 在一个比例中,两个外项互为倒数,其中一个内项是412,另一个内项是______.
- 根据8×9=12×6写出的比例,正确的是[ ]A.9:12=8:6B.8:12=9:6C.9:12=6:8