本试题 “(本小题满分14分)已知平面向量=(,-1),=(x,y)(x>0),=1.(Ⅰ)若对任意实数t都有,求向量;(Ⅱ)令=+(sin2α-2cos2α),=(sin22α)+(cos2α),α∈(,π),若⊥,,求t...” 主要考查您对向量数量积的含义及几何意义
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 向量数量积的含义及几何意义
两个向量的夹角的定义:
对于非零向量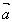 ,
,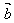 ,作
,作 称为向量
称为向量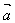 ,
,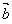 的夹角,当
的夹角,当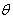 =0时,
=0时,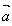 ,
,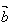 同向,当
同向,当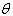 =π时,
=π时,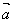 ,
,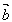 反向,
反向,
当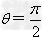 时,
时,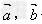 垂直。
垂直。
两个向量数量积的含义:
如果两个非零向量 ,
, ,它们的夹角为
,它们的夹角为 ,我们把数量
,我们把数量 叫做
叫做 与
与 的数量积(或内积或点积),记作:
的数量积(或内积或点积),记作: ,即
,即 。
。 叫
叫 在
在 上的投影。
上的投影。
规定:零向量与任一向量的数量积是0,注意数量积是一个实数,不再是一个向量。
两个向量数量积的几何意义:
数量积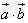 等于
等于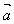 的模
的模 与
与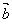 在
在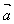 上的投影
上的投影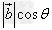 的乘积。
的乘积。
向量数量积的性质:
设两个非零向量
(1) ;
;
(2) ;
;
(3) ;
;
(4) ;
;
(5)当 ,
, 同向时,
同向时, ;当
;当 与
与 反向时,
反向时, ;当
;当 为锐角时,
为锐角时, 为正且
为正且 ,
, 不同向,
不同向, ;当
;当 为钝角时,
为钝角时, 为负且
为负且 ,
, 不反向,
不反向, 。
。
发现相似题
与“(本小题满分14分)已知平面向量=(,-1),=(x,y)(x>0),=1.(...”考查相似的试题有:
- 已知向量,若垂直,则的值为A.B.C.D.
- 已知向量若,则与的夹角为( )A.30°B.60°C.120°D.150°
- (本小题满分10分)(注意:在试题卷上作答无效)的三个内角A,B,C所对的边分别为a,b,c, 向量且(Ⅰ)求的大小;(Ⅱ)现给出下列四...
- 在中,点O为BC的中点,过O的直线分别交直线AB,AC于不同的两点M,N若,则的值为
- 若向量的夹角为,,则= ;
- 已知向量a=(,1),b是不平行于x轴的单位向量,且a·b=,则b等于( )A.B.C.D.(1,0)
- 已知中,平面内一点满足,若,则的值为A.3B.C.2D.
- 若函数的图象与x轴交于点,过点的直线与函数 的图象交于两点,则 ( )A.B.16C.32D.
- 设a=(4,3),a在b上的投影为,b在x轴上的投影为2,且|b|≤14,则b为[ ]A.(2,14)B.C.D.(2,8)
- 如图,在中,,延长到,使,若,则 的值是 ( )A.B.C.D.