本试题 “下列命题:①若a•b=0,则a=0或b=0;②若|a|=|b|,则a=b或a=-b;③|a-b|2=|a|2-2|a||b|+|b|2;④(a-b)•(a+b)=|a|2-|b|2.其中,正确命题的序号是 ______.(把所有...” 主要考查您对向量数量积的含义及几何意义
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 向量数量积的含义及几何意义
两个向量的夹角的定义:
对于非零向量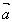 ,
,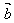 ,作
,作 称为向量
称为向量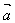 ,
,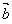 的夹角,当
的夹角,当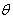 =0时,
=0时,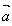 ,
,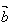 同向,当
同向,当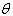 =π时,
=π时,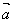 ,
,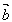 反向,
反向,
当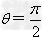 时,
时,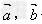 垂直。
垂直。
两个向量数量积的含义:
如果两个非零向量 ,
, ,它们的夹角为
,它们的夹角为 ,我们把数量
,我们把数量 叫做
叫做 与
与 的数量积(或内积或点积),记作:
的数量积(或内积或点积),记作: ,即
,即 。
。 叫
叫 在
在 上的投影。
上的投影。
规定:零向量与任一向量的数量积是0,注意数量积是一个实数,不再是一个向量。
两个向量数量积的几何意义:
数量积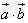 等于
等于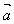 的模
的模 与
与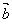 在
在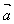 上的投影
上的投影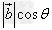 的乘积。
的乘积。
向量数量积的性质:
设两个非零向量
(1) ;
;
(2) ;
;
(3) ;
;
(4) ;
;
(5)当 ,
, 同向时,
同向时, ;当
;当 与
与 反向时,
反向时, ;当
;当 为锐角时,
为锐角时, 为正且
为正且 ,
, 不同向,
不同向, ;当
;当 为钝角时,
为钝角时, 为负且
为负且 ,
, 不反向,
不反向, 。
。
发现相似题
与“下列命题:①若a•b=0,则a=0或b=0;②若|a|=|b|,则a=b或a=-b;...”考查相似的试题有:
- 若向量与的夹角是,,且 则
- 已知向量,,若向量,则A.2B.C. 8D.
- 已知向量,满足||="2," ||=l,且(+)⊥(),则与的夹角为A.B.C.D.
- 如图,在中,,是边上一点,,则 .
- 如图,在平行四边形中,,垂足为,, 点是内(包括边界)的动点,则的取值范围是 .
- 已知点为所在平面上的一点,且,其中为实数,若点落在的内部,则的取值范围是 .
- 已知△ABC中,点A、B、C的坐标依次是A(2,-1),B(3,2),C(-3,-1),BC边上的高为AD,则的坐标是:_______.
- (02年新课程高考天津卷)已知两点M(-1,0),N(1,0),且点P使·,·,·成公差小于零的等差数列(1)点P的轨迹是什么曲线?...
- (本题满分13分)已知向量(Ⅰ)当时,求函数的值域;(Ⅱ)若的值.
- ( )A.B.C.D.