本试题 “如图是小明“探究斜面的机械效率与倾斜程度关系”的实验装置,他在实验时用弹簧测力计拉着重为6N的木块分别沿倾斜程度不同的同一斜面匀速向上运动,实验数据记...” 主要考查您对功的计算公式的应用
有用功和额外功
斜面的机械效率
其他简单机械:轮轴和斜面
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 功的计算公式的应用
- 有用功和额外功
- 斜面的机械效率
- 其他简单机械:轮轴和斜面
应用:
利用功的计算公式加计算:F或S,F=W/s,s=W/F。
转换思想求功的大小 :
“转换思想方法”求功的大小。公式W=Fs中的s 必须是在力的方向通过的距离,而且F的大小一直保持不变,能运用功的公式求解,当作用在物体上的力的大小总在发生改变,则在求解功的时候注意不能直接利用公式W=Fs,应转换思想。如:平放在地上的一根均匀木料,现用一总垂直木料方向的力将它抬到竖直为止,则至少要做多少功?由于抬木料的力的大小、方向总在发生改变,而且木料通过的距离也不完全在力的方向上,故无法直接应用公式求解。我们根据功的原理可知:使用任何机械都不省功,则对物体所做的功等效于将物体重心提高所做的功,即可求解。
例:小明同学用一个距离手3m高的定滑轮拉住重100N的物体,从滑轮正下方沿水平方向移动4m如图所示,若不计绳重和摩擦,他至少做功( )
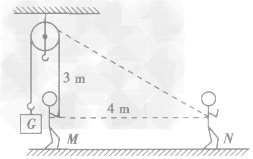
A.200JB.300J C.400JD.500J
解析:本题中由于不计绳重和摩擦,属于理想机械,可使用功的原理进行求解。人站在M处时,绳长3m,当人走到N处时,此时的绳长由勾股定理可知为5m,也就是说人从M点走到N点拉下的长度为2m,即物体上升的高度h=2m。小明对绳做功至少是克服物重G所做的功,即W=Gh=100N×2m=200J。
答案:A
利用功的计算公式加计算:F或S,F=W/s,s=W/F。
转换思想求功的大小 :
“转换思想方法”求功的大小。公式W=Fs中的s 必须是在力的方向通过的距离,而且F的大小一直保持不变,能运用功的公式求解,当作用在物体上的力的大小总在发生改变,则在求解功的时候注意不能直接利用公式W=Fs,应转换思想。如:平放在地上的一根均匀木料,现用一总垂直木料方向的力将它抬到竖直为止,则至少要做多少功?由于抬木料的力的大小、方向总在发生改变,而且木料通过的距离也不完全在力的方向上,故无法直接应用公式求解。我们根据功的原理可知:使用任何机械都不省功,则对物体所做的功等效于将物体重心提高所做的功,即可求解。
例:小明同学用一个距离手3m高的定滑轮拉住重100N的物体,从滑轮正下方沿水平方向移动4m如图所示,若不计绳重和摩擦,他至少做功( )

A.200JB.300J C.400JD.500J
解析:本题中由于不计绳重和摩擦,属于理想机械,可使用功的原理进行求解。人站在M处时,绳长3m,当人走到N处时,此时的绳长由勾股定理可知为5m,也就是说人从M点走到N点拉下的长度为2m,即物体上升的高度h=2m。小明对绳做功至少是克服物重G所做的功,即W=Gh=100N×2m=200J。
答案:A
有用功,额外功与总功:
区分有用功和额外功:
区分有用功与额外功的关键是看我们需要达到什么做功目的。在同一做功过程中,目的不同,功的性质就不一样。例如:用桶将水从水井中提出来,提水是我们需要的,而提桶是不需要,但又不得不做的功,故克服水重做的是有用功,而克服桶重做的是额外功;如果是一只桶掉入水井里,我们要将桶从井中提出来,则克服桶重做的是有用功,而克服桶中可能带出来的水的重力所做的功就是额外功了。
| 名称 | 定义 | 符号 | 公式 | 实例 |
| 有用功 | 使用机械做功时对人们有用的功 | W有 | W有=Gh | 从井中打水时提水所做的功 |
| 额外功 | 对人们没有用但又不得不做的功 | W额 | —— | 从井中打水时提水桶和绳子所做的功 |
| 总功 | 有用功与额外功之和 | W总 | W总=W有+W额 | 从井中打水时手的拉力所做的功 |
区分有用功和额外功:
区分有用功与额外功的关键是看我们需要达到什么做功目的。在同一做功过程中,目的不同,功的性质就不一样。例如:用桶将水从水井中提出来,提水是我们需要的,而提桶是不需要,但又不得不做的功,故克服水重做的是有用功,而克服桶重做的是额外功;如果是一只桶掉入水井里,我们要将桶从井中提出来,则克服桶重做的是有用功,而克服桶中可能带出来的水的重力所做的功就是额外功了。
计算有用功,额外功和总功的方法:
1. 总功的计算:
(1)定义法:W总=Fs
(2)总功等于有用功和额外功之和,即W总=W有用+W额外
(3)公式法:
2. 有用功的计算方法:
(1)定义法:W有用=Gh
(2)W有用=W总-W额外
(3)公式法: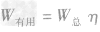
3. 额外功的计算方法:
(1)定义法: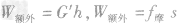
(2)W额外=W总-W有用
(3)公式法: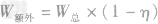
斜面的机械效率:
测量斜面的机械效率:
【实验目的】:测量斜面的机械效率
【器材】斜面,铁架台,小车,弹簧秤,米尺
【操作】
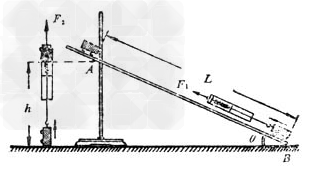
(1)照图那样安装好斜面,将小车放在斜面上。用弹簧秤缓慢地把小车拉上斜面,记下弹簧秤的示数F,测出小车沿斜面通过的距离L,用弹簧秤称得小车重G,并测出小车上升的高度h,算出斜面的效率η1=Gh/FL。
(2)把小车翻过来(轮子朝上)放在斜面上,重复上述实验,根据实验数据算出此时斜面效率η2。
(3)增大斜面的倾角,小车仍翻着放在斜面上重复实验,算出斜面效率η3。
比较η1、η2、η3的大小,可知η1>η2,η2<η3。分析实验结果可得:斜面的效率主要受斜面和小车间的摩擦的影响,在(1)中由于轮子和斜面间的滚动摩擦小,必需做的额外功少,效率就高。在(3)中,当倾角增大,车对斜面的压力减小,从而摩擦也减小,因此效率比(2)时高。比较操作(2)、(3)中的F及η的大小,可知斜面越省力其效率不一定越高。
提高斜面机械效率的方法:
在其他条件一定时,斜面的倾斜程度越大,机械效率越高,斜面表面粗糙程度越大,机械效率越低;机械效率与物体重量无关,物体斜面之间接触面大小无关。
例:如图所示,斜面高为1m,长为3m,工人用 400N沿斜面方向的力将重为840N的箱子拉到汽车上,在这过程中拉力做了______J的功,机械效率为______。要提高该斜面的机械效铝,应该_______。(写出一条措施)

解析: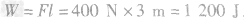 ,
,
提高机械效率的方法是减小总功,以增大有用功在总功中所占的比例。
答案:1200 70% 减小斜面的粗糙度
| 有用功 | W有用=Gh |
| 总功 | W总=Fl W总=Gh+fl (f为摩擦力) |
| 额外功 | W额外=W总-W有用 W额外=fl |
| 机械效率 |  |
测量斜面的机械效率:
【实验目的】:测量斜面的机械效率
【器材】斜面,铁架台,小车,弹簧秤,米尺
【操作】

(1)照图那样安装好斜面,将小车放在斜面上。用弹簧秤缓慢地把小车拉上斜面,记下弹簧秤的示数F,测出小车沿斜面通过的距离L,用弹簧秤称得小车重G,并测出小车上升的高度h,算出斜面的效率η1=Gh/FL。
(2)把小车翻过来(轮子朝上)放在斜面上,重复上述实验,根据实验数据算出此时斜面效率η2。
(3)增大斜面的倾角,小车仍翻着放在斜面上重复实验,算出斜面效率η3。
比较η1、η2、η3的大小,可知η1>η2,η2<η3。分析实验结果可得:斜面的效率主要受斜面和小车间的摩擦的影响,在(1)中由于轮子和斜面间的滚动摩擦小,必需做的额外功少,效率就高。在(3)中,当倾角增大,车对斜面的压力减小,从而摩擦也减小,因此效率比(2)时高。比较操作(2)、(3)中的F及η的大小,可知斜面越省力其效率不一定越高。
提高斜面机械效率的方法:
在其他条件一定时,斜面的倾斜程度越大,机械效率越高,斜面表面粗糙程度越大,机械效率越低;机械效率与物体重量无关,物体斜面之间接触面大小无关。
例:如图所示,斜面高为1m,长为3m,工人用 400N沿斜面方向的力将重为840N的箱子拉到汽车上,在这过程中拉力做了______J的功,机械效率为______。要提高该斜面的机械效铝,应该_______。(写出一条措施)

解析:
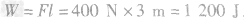 ,
,
提高机械效率的方法是减小总功,以增大有用功在总功中所占的比例。
答案:1200 70% 减小斜面的粗糙度
轮轴定义:
由两个半径不等的圆柱固定在同一轴线上组成,大的称为轮,小的称为轴。(如图)
斜面定义:
是一个与水平面成一定夹角的倾斜平面:是一种省力的简单机械。
轮轴:
1.轮轴的实质:是—个可以连续转动的杠杆。(如图)
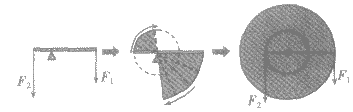
2.轮轴的特点:轮半径是轴半径的几倍,加在轮上的力就是加在轴上的力的几分之一。即:
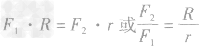
3.轮轴的功能:一是改变用力的大小;二是改变物体的运动速度。
4.生活中的轮轴:如:辘轳、汽车方向盘、门把手、扳手等。
斜面:
特点:因为斜面是一种省力的简单机械(如图所示)。若忽略摩擦,斜面长是斜面高的n倍,拉力就是物体所受重力的n分之一。即:
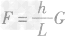
F一沿斜面拉力
G一物体重力
L一斜面长
h一斜面高
从公式中可知:斜面越长,越省力。
发现相似题
与“如图是小明“探究斜面的机械效率与倾斜程度关系”的实验装置,...”考查相似的试题有:
- 使用自重可以忽略的动滑轮提起50N的重物,人对绳做的功是100J,则人对绳的最小拉力为______N,动滑轮把物体提起的高度为_____...
- 2004年9月26日,首届F1中国大奖赛在上海国际赛车场“上字型”赛道上隆重举行.比赛吸引了14余万车迷到场观看,最后,法拉利车队...
- 小文同学在“测定滑轮组机械效率”的实验中,用如图所示的装置匀速吊起钩码,并记录了如下实验数据:根据实验数据,完成如下问...
- 小强用如图所示的滑轮组匀速拉动物体A,使重为2000N的物体A在3s内沿水平方向匀速移动了6m,若A所受地面的摩擦力f=600N,小强...
- 一台功率为40kw的抽水机,机械效率为60%,如果要把河水抽到5m高的地方,则每小时抽水机做的总功是______J,其中有用功是_____...
- 工人用定滑轮将重为180N的物体匀速提升2m,所用的拉力为200N.此过程中有用功是______,额外功是______,机械效率为______.
- 和谐社会处处体现人性化的生活细节,比如在许多单位的门口都设有专供残疾人轮椅通行的坡道(如图所示),从物理学的角度分析...
- 日常生活中常用简单机械有:A、剪铁皮的剪刀;B、天平;C、钓鱼杆;D、起钉子用的羊角锤;E、镊子;F、缝纫机脚踏板;G、汽车...
- 关于使用简单机械,下列说法正确的是( )A.使用斜面,可以省力B.使用滑轮组,可以省功C.使用等臂杠杆,可以省距离D.使用...
- 有两个高度相同的螺钉,螺纹越密的螺钉越______ (填“省力”或“费力”);这是由于______.