本试题 “如图甲所示,水平传送带顺时针方向匀速运动。从传送带左端P先后由静止轻轻放上三个物体A、B、C,物体A经tA=9.5s到达传送带另一端Q,物体B经tB=10s到达传送...” 主要考查您对v-t图像
从运动情况确定受力
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- v-t图像
- 从运动情况确定受力
v—t图像:
物体的运动速度与时间的关系可以用图像来描述。以速度V为纵轴、时间T为横轴建立坐标系,再根据相关数据进项描点,用平滑的曲线将连依次连接起来,就建立了速度时间图象,也就是VT图像。
v—t图像的含义:
1、v-t图象描述速度随时间的变化规律;
2、在速度图像中,可以读出物体在任何时刻的速度;
3、在速度图像中,物体在一段时间内的位移大小等于物体的速度图像与这段时间轴所围面积的值;
4、在速度图像中,物体在任意时刻的加速度就是速度图像上所对应的点的切线的斜率;
5、图线与横轴交叉,表示物体运动的速度反向;
6、图线是直线表示物体做匀变速直线运动或匀速直线运动;图线是曲线表示物体做变加速运动。
知识点拨:
 图一
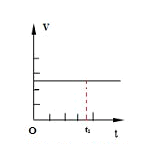
图一
图一是匀速直线运动的v—t的图像,其函数关系式为:v=v,匀速直线运动的物体的速度v是个恒量与路程S和时间t没关系。一段时间(t)内,走过的路程(S),满足关系式:S=vt,在图像中为一矩形包围的面积。
 图二
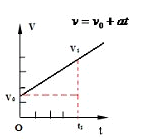
图二
图二是初速度不为0的匀加速直线运动的v—t图像,其函数关系式为: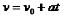 ,匀加速直线运动的物体运动的加速度a(直线的斜率)是个恒量,初速度
,匀加速直线运动的物体运动的加速度a(直线的斜率)是个恒量,初速度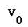 也是恒量,与路程S和时间t没关系。一段时间(t)内,走过的路程(S),满足关系式:
也是恒量,与路程S和时间t没关系。一段时间(t)内,走过的路程(S),满足关系式: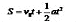 ,在图像中为“矩形+三角形”所包围的面积。
,在图像中为“矩形+三角形”所包围的面积。
v-t图像的基本类型:
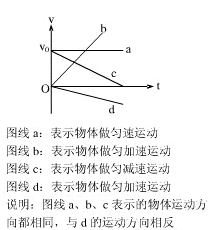
从运动情况确定受力:
1、知道物体的运动情况,应用运动学公式求出物体的加速度,再应用牛顿第二定律,推断或者求出物体的受力情况。
2、分析这类问题的关键是抓住受力情况和运动情况的桥梁——加速度。
3、求解动力学这两类问题的思路,可由下面的框图来表示。
瞬时加速度问题的解决方法:
分析物体在某一时刻的瞬时加速度,关键是分析瞬时前后的受力情况及运动状态,再由牛顿第二定律求出瞬时加速度。此类问题应注意以下两种基本模型。
(1)刚性绳(或接触面):可认为是一种不发生明显形变就能产生弹力的物体。若剪断(或脱离)后,其弹力立即消失,不需要考虑形变恢复时间。一般题目中所给的细绳(线)和接触面,在不加特殊说明时,均可按此模型处理。解决此模型的关键在于分析情景突变后的过程,利用过程的初状态分析求解状态突变后的瞬时加速度。
(2)弹簧(或橡皮绳):此类物体的特点是形变量大,形变恢复需要较长时间。在瞬时问题中,其弹力的大小往往可以看成不变。但当弹簧的一端不与有质量的物体连接时,轻弹簧的形变不需要时间,弹力可以突变。解决此类问题时需利用情景突变前的受力来确定情景突变后瞬间的受力及加速度。
动力学范围的整体法与隔离法:
处理连接体问题的方法有整体法和隔离法。
1.整体法将一组连接体作为一个整体看待,牛顿第二定律中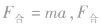 是整体受的合外力,只分析整体所受的外力即可(因为连接体的相互作用力是内力,可不分析),简化了受力分析。在研究连接体时,连接体各部分的运动状态可以相同,也可以不同。当连接体各部分运动状态不同时,整体的合外力等于各部分质量与各部分加速度乘积的矢量和,即F合
是整体受的合外力,只分析整体所受的外力即可(因为连接体的相互作用力是内力,可不分析),简化了受力分析。在研究连接体时,连接体各部分的运动状态可以相同,也可以不同。当连接体各部分运动状态不同时,整体的合外力等于各部分质量与各部分加速度乘积的矢量和,即F合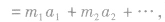 写成分量形式有:
写成分量形式有: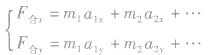
如果待求的问题不涉及系统内部的相互作用时,就可以采用整体法。
2.隔离法在求解连接体的相互作用力时采用,将某个部分从连接体中分离出来,其他部分对它的作用力就成了外力。
整体法与隔离法在研究连接体问题时经常交替使用。
与“如图甲所示,水平传送带顺时针方向匀速运动。从传送带左端P先...”考查相似的试题有:
- t =0时两辆汽车在平直公路上的同一位置,向同一方向行驶,v-t图线如图中甲、乙所示,可以确定[ ]A.乙车始终在甲车前方B.乙...
- 物体由静止开始做加速度为1m/s2的匀加速直线运动,4s后加速度大小变为0.5 m/s2,方向与原来方向相反。请做出它在8s内的v-t图...
- 从同一地点同时开始沿同一直线运动的两个物体Ⅰ、Ⅱ的速度-时间图象如图所示。在0~t2时间内,下列说法中正确的是[ ]A.Ⅰ物体所...
- 在空气阻力大小恒定的条件下,小球从空中下落,与水平地面相碰后弹到空中某一高度,以向下为正方向,其速度随时间变化的关系如图...
- 甲和乙两个物体在同一直线上运动,它们的v-t图像分别如图中的a和b所示,在t1时刻[ ]A.它们的运动方向相同B.它们的运动方向...
- 放置在光滑地面上的物体在某种力的作用下从静止开始向右运动,如果该物体的速度时间图像是一条抛物线,如图所示,则下列说法...
- 北京时间2011年2月18日晚6时,在经历了260天的密闭飞行后,中国志愿者王跃走出“火星-500”登陆舱,成功踏上模拟火星表面,在“...
- 如图所示,小车板面上的物体质量为m=8kg,它被一根水平方向上拉伸了的弹簧拉住而静止在小车上,这时弹簧的弹力为6N。现沿水平...
- 质量为0.3kg的物体在水平面上运动,图中的两条直线分别表示物体受水平拉力和不受水平拉力的v-t图象,则下列说法中不正确的是[...
- 如图所示,木块A质量为1kg,木块B的质量为2kg,叠放在水平地面上,AB间的最大静摩擦力为1N,B与地面间的动摩擦因数为0.1,今...