某高级中学共有学生3000名，各年级男、女生人数如下表：已知在全校学生中随机抽取1名，抽到高二年级女生的概率是0.18．（I）问高二年级有多,高中三年级,数学试题,分层抽样考点,古典概型的定义及计算考点,好技网

本试题 “某高级中学共有学生3000名，各年级男、女生人数如下表：已知在全校学生中随机抽取1名，抽到高二年级女生的概率是0.18．（I）问高二年级有多少名女生？（II）...” 主要考查您对
分层抽样

古典概型的定义及计算
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。

分层抽样：

当已知总体由差异明显的几部分组成时，常将总体分成几部分，然后按照各部分所占的比例进行抽样，这种抽样叫做分层抽样，其所分成的各个部分叫做层。
利用分层抽样抽取样本，每一层按照它在总体中所占的比例进行抽取。

不放回抽样和放回抽样:

在抽样中，如果每次抽出个体后不再将它放回总体，称这样的抽样为不放回抽样；如果每次抽出个体后再将它放回总体，称这样的抽样为放回抽样．
随机抽样、系统抽样、分层抽样都是不放回抽样

分层抽样的特点：

（1）分层抽样适用于差异明显的几部分组成的情况；
（2）在每一层进行抽样时，在采用简单随机抽样或系统抽样；
（3）分层抽样充分利用已掌握的信息，使样具有良好的代表性；
（4）分层抽样也是等概率抽样，而且在每层抽样时，可以根据具体情况采用不同的抽样方法，因此应用较为广泛。

常用的抽样方法及它们之间的联系和区别：

类别	共同点	各自特点	相互联系	适用范围
简单随机抽样	抽样过程中每个个体被抽取的概率是相同的	从总体中逐个抽取		总体中的个体个数少
系统抽样		将总体均匀分成几个部分，按照事先确定的规则在各部分抽取	在起始部分抽样时采用简单随机抽样	总体中的个体个数多
分层抽样		将总体分成几层，分层进行抽取	各层抽样时采用简单抽样或者相同抽样	总体由差异明显的几部分组成

基本事件的定义：

一次试验连同其中可能出现的每一个结果称为一个基本事件。

等可能基本事件：

若在一次试验中，每个基本事件发生的可能性都相同，则称这些基本事件为等可能基本事件。

古典概型：

如果一个随机试验满足：（1）试验中所有可能出现的基本事件只有有限个；
（2）每个基本事件的发生都是等可能的；
那么，我们称这个随机试验的概率模型为古典概型．

古典概型的概率：

如果一次试验的等可能事件有n个，那么，每个等可能基本事件发生的概率都是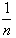；如果某个事件A包含了其中m个等可能基本事件，那么事件A发生的概率为
。

古典概型解题步骤：

（1）阅读题目，搜集信息；
（2）判断是否是等可能事件，并用字母表示事件；
（3）求出基本事件总数n和事件A所包含的结果数m；
（4）用公式求出概率并下结论。

求古典概型的概率的关键：

求古典概型的概率的关键是如何确定基本事件总数及事件A包含的基本事件的个数。

发现相似题

与“某高级中学共有学生3000名，各年级男、女生人数如下表：已知...”考查相似的试题有：