本试题 “如图,有一底角为35的等腰三角形纸片,现过底边上一点,沿与底边垂直的方向将其剪开,分成三角形和四边形两部分,则四边形中,最大角的度数是( ).” 主要考查您对三角形的内角和定理
等腰三角形的性质,等腰三角形的判定
多边形的内角和和外角和
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 三角形的内角和定理
- 等腰三角形的性质,等腰三角形的判定
- 多边形的内角和和外角和
三角形的内角和定理及推论:
三角形的内角和定理:三角形三个内角和等于180°。
推论:
(1)直角三角形的两个锐角互余。
(2)三角形的一个外角等于和它不相邻的来两个内角的和。
(3)三角形的一个外角大于任何一个和它不相邻的内角。
注:在同一个三角形中:等角对等边;等边对等角;大角对大边;大边对大角。
三角形的内角和定理:三角形三个内角和等于180°。
推论:
(1)直角三角形的两个锐角互余。
(2)三角形的一个外角等于和它不相邻的来两个内角的和。
(3)三角形的一个外角大于任何一个和它不相邻的内角。
注:在同一个三角形中:等角对等边;等边对等角;大角对大边;大边对大角。
定义:
有两条边相等的三角形,是等腰三角形,相等的两条边叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角。
有两条边相等的三角形,是等腰三角形,相等的两条边叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角。
等腰三角形的性质:
1.等腰三角形的两个底角度数相等(简写成“等边对等角”)。
2.等腰三角形的顶角的平分线,底边上的中线,底边上的高重合(简写成“等腰三角形的三线合一”)。
3.等腰三角形的两底角的平分线相等(两条腰上的中线相等,两条腰上的高相等)。
4.等腰三角形底边上的垂直平分线到两条腰的距离相等。
5.等腰三角形的一腰上的高与底边的夹角等于顶角的一半。
6.等腰三角形底边上任意一点到两腰距离之和等于一腰上的高(需用等面积法证明)。
7.等腰三角形是轴对称图形,只有一条对称轴,顶角平分线所在的直线是它的对称轴,等边三角形有三条对称轴。
8.等腰三角形中腰的平方等于高的平方加底的一半的平方
9.等腰三角形中腰大于高
10.等腰三角形底边延长线上任意一点到两腰距离之差等于一腰上的高(需用等面积法证明)
等腰三角形的判定:
1.定义法:在同一三角形中,有两条边相等的三角形是等腰三角形。
2.判定定理:在同一三角形中,有两个角相等的三角形是等腰三角形(简称:等角对等边)。
3.顶角的平分线,底边上的中分线,底边上的高的重合的三角形是等腰三角形。
在平面内,由若干不在同一直线上的线段首尾顺次连接组成的封闭图形叫做多边形。
对角线:在多边形中,连接不相邻的两个顶点的线段叫做多边形的对角线。
外角:多边形的一边与另一边的反向延长线所组成的角叫做这个多边形的外角。
如图示:
多边形的内角和:
n边形的内角和等于(n-2)·180°。(多边形内角和定理)
多边形的外角和:
在多边形的每个顶点处取多边形的一个外角,它们的和叫做多边形的外角和。
多边形的外角和等于360°。(与边数无关) (多边形的外角和定理)
多边形外角和列举: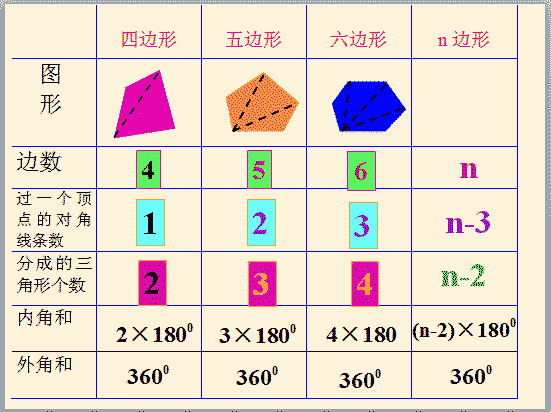
发现相似题
与“如图,有一底角为35的等腰三角形纸片,现过底边上一点,沿与...”考查相似的试题有:
- 已知等腰三角形的一边等于3cm,别一边等于5cm,则周长为______cm.
- 如图1,在平面直角坐标系中,等腰Rt△AOB的斜边OB在x轴上,直线y=3x-4经过等腰Rt△AOB的直角顶点A,交y轴于C点,双曲线也经过A...
- 在等腰三角形ABC中,∠A=120°,则∠B=______.
- (1)在三角形ABC中,∠C=90°,则有AB2=AC2+BC2.例如:当AC=6,BC=8,∠C=90°时,AB2=62+82=100,∴AB=10(如图1),根据上述方...
- 如图,∠CDG=∠B,AD平分∠ABC,请说明△AGD是等腰三角形,请将过程填写完整.∵∠CDG=∠B (______)∴DG∥AB (______)∴∠1=______ ...
- 等腰三角形的底边长为6,底边上的中线长为4 ,它的腰长为[ ]A.7B.6C.5D.4
- 已知一个等腰三角形的一边长为5,另一边长为7,则这个等腰三角形的周长为( )。
- 一个多边形的每一个内角都等于150°,则这个多边形的边数是( )A.八B.十C.十二D.十五
- 若一个多边形的内角和等于1080°,则这个多边形的边数是[ ]A.9 B.8 C.7 D.6
- 已知n边形的内角和与外角和之比为9:2,则n=______.