本试题 “(1)当m取何值时,函数y=为反比例函数?(2)已知函数y=(m2-m-2)x,y可能是x的反比例函数吗?y可能是x的正比例函数吗?” 主要考查您对正比例函数的定义
反比例函数的定义
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 正比例函数的定义
- 反比例函数的定义
正比例函数定义:
一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数。
正比例函数属于一次函数,但一次函数却不一定是正比例函数。
正比例函数是一次函数的特殊形式,即一次函数y=kx+b中,若b=0,即所谓“y轴上的截距”为零,则为正比例函数。
正比例函数的关系式表示为:y=kx(k为比例系数)
当k>0时(一三象限),k越大,图像与y轴的距离越近。函数值y随着自变量x的增大而增大。
当k<0时(二四象限),k越小,图像与y轴的距离越近。自变量x的值增大时,y的值则逐渐减小。
一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数。
正比例函数属于一次函数,但一次函数却不一定是正比例函数。
正比例函数是一次函数的特殊形式,即一次函数y=kx+b中,若b=0,即所谓“y轴上的截距”为零,则为正比例函数。
正比例函数的关系式表示为:y=kx(k为比例系数)
当k>0时(一三象限),k越大,图像与y轴的距离越近。函数值y随着自变量x的增大而增大。
当k<0时(二四象限),k越小,图像与y轴的距离越近。自变量x的值增大时,y的值则逐渐减小。
正比例函数性质:
定义域
R(实数集)
值域
R(实数集)
奇偶性
奇函数
单调性
当k>0时,图像位于第一、三象限,从左往右,y随x的增大而增大(单调递增),为增函数;
当k<0时,图像位于第二、四象限,从左往右,y随x的增大而减小(单调递减),为减函数。
周期性
不是周期函数。
对称性
对称点:关于原点成中心对称
对称轴:自身所在直线;自身所在直线的垂直平分线
一般地,函数 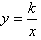 (k是常数,k≠0)叫做反比例函数,自变量x的取值范围是x≠0的一切实数,函数值的取值范围也是一切非零实数。
(k是常数,k≠0)叫做反比例函数,自变量x的取值范围是x≠0的一切实数,函数值的取值范围也是一切非零实数。
注:
(1)因为分母不能为零,所以反比例函数函数的自变量x不能为零,同样y也不能为零;
(2)由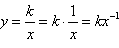 ,所以反比例函数可以写成
,所以反比例函数可以写成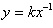 的形式,自变量x的次数为-1;
的形式,自变量x的次数为-1;
(3)在反比例函数中,两个变量成反比例关系,即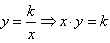 ,因此判定两个变量是否成反比例关系,应看是否能写成反比例函数的形式,即两个变量的积是不是一个常数。
,因此判定两个变量是否成反比例关系,应看是否能写成反比例函数的形式,即两个变量的积是不是一个常数。
表达式:
x是自变量,y是因变量,y是x的函数
自变量的取值范围:
①在一般的情况下,自变量x的取值范围可以是不等于0的任意实数;
②函数y的取值范围也是任意非零实数。
反比例函数性质:
①反比例函数的表达式中,等号左边是函数值y,等号右边是关于自变量x的分式,分子是不为零的常数k,分母不能是多项式,只能是x的一次单项式;
②反比例函数表达式中,常数(也叫比例系数)k≠0是反比例函数定义的一个重要组成部分;
③反比例函数 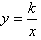 (k是常数,k≠0)的自变量x的取值范围是不等式0的任意实数,函数值y的取值范围也是非零实数。
(k是常数,k≠0)的自变量x的取值范围是不等式0的任意实数,函数值y的取值范围也是非零实数。
发现相似题
与“(1)当m取何值时,函数y=为反比例函数?(2)已知函数y=(m2...”考查相似的试题有:
- 函数y=k(x-1)的图象向左平移一个单位后与反比例函数y=的图象的交点为A、B,若点A的坐标为(1,2),则点B的坐标为_______.
- 函数y=(2-k)x是正比例函数,则k的取值范围是______.
- 一次函数的图象与y轴交于点,且与两坐标轴围成的三角形面积是20,求该一次函数的解析式。
- 进入三月以来,重庆的气温渐渐升高,羽绒服进入了销售淡季。为此重庆某百货公司对某品牌的A款羽绒服进行了清仓大处理。已知A...
- 某地区一种商品的需求量(万件)、供应量(万件)与价格(元/件)分别近似满足下列函数关系式:,.需求量为时,即停止供应...
- 若一次函数y=kx+b的函数值y随x的增大而减小,且图象与y轴的正半轴相交,那么 对k和b的符号判断正确的是…………………………………………………(...
- 若正比例函数的图像经过点(-1,2),则这个图像必经过点( )A.(1,2)B.(-1,-2)C.(2,-1)D.(1,-2)
- 已知反比例函数(1)若点A(1,2)在这个函数的图像上,求k的值;(2)若在这个函数图像的每一分支上,y随x的增大而减小,求k...
- 关于函数,下列结论正确的是 ( )A.函数图像必经过点(1,2)B.函数图像经过二、四象限C.y随x的增大而增大D.y随x的增大...
- 如果函数y=kxk2-2的图象是双曲线,且在第二、四象限内,那么k的值是______.