本试题 “若a、b互为相反数,则在①a+b=0,②|a|=|b|,③a2=b2,④a3=b3,⑤ab=-b2中,必定成立的个数为[ ]A.2个B.3个C.4个D.5个” 主要考查您对相反数
等式的性质
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 相反数
- 等式的性质
相反数的定义:
像2和-2,5和-5这样,只有符号不同的两个数叫做互为相反数。
相反数的几何意义:在数轴上到原点距离相等的两个点表示的两个数叫做互为相反数。
相反数的代数意义:如果两个数的和为零,其中一个数是另一个数的相反数,这两个数称为互为相反数。
相反数的特性:
1、若a,b互为相反数,则a+b=0; 反之,若a+b=0,则a,b互为相反数;
2、在数轴上,互为相反数(0除外)的两个点位于原点的两旁,并且关于原点对称;
3、此时,b的相反数为﹣b=﹣(﹣a)=a,那么我们就说“相反数具有互称性”。
4、相反数的规律:正数的相反数是负数,负数的相反数是正数,0的相反数是0。
5、相反数的表示方法:a的相反数是-a,-a的相反数是a;a-b的相反数是b-a,b-a的相反数是a-b;a+b的相反数是-(a+b),即-a-b。
(互为)相反数的代数意义:
1、只有符号不同的两个数称互为相反数。a和-a是一对互为相反数,a叫做-a的相反数,-a叫做a的相反数。注意:-a不一定是负数。a不一定是正数。(a不等于0)
2、若两个实数a和b满足b=﹣a。我们就说b是a的相反数。
3、两个互为相反数的实数a和b必满足a+b=0。也可以说实数a和b满足a+b=0,则这两个实数a,b互为相反数。
相反数的判别:
我们在利用相反数的概念进行化简时,很多情况下,把括号里的部分看成一个整体(即想象成一个数a),问题就容易解决。因此要求一个数的相反数,只要在这个数前面叫上“-”,再化简即可。
多重符号的化简:
1、在一个数前面添加一个“+”好,所得的数与原数相同。
2、在一个数前面添加一个“-”号,所得的数就成为原数的相反数。
3、对于有三个火三个以上符号的数的化简,首先要注意,一个数前面不管有多少个“+”号,可以把正号去掉,其次要看“-”号的个数,当“-”号的个数为偶数个时,结果取正,当“-”号的个数为奇数个时,结果取“-”号。
等式:
含有等号的式子叫做等式(数学术语)。
形式:把相等的两个数(或字母表示的数)用“=”连接起来。
等式可分为矛盾等式和条件等式。矛盾等式就是左右两边不相等的"等式"。也就是不成立的等式,比如5+2=8,实际上5+2=7,所以5+2=8是一个矛盾等式.有些式子无法判断是不是矛盾等式,比如x-9=2,只有x=11时这个等式才成立(这样的等式叫做条件等式),x≠11时,这个等式就是矛盾等式。
等式的性质:
1.等式两边同加上(或减去)同一个数或同一个整式,所得结果仍是等式。
即若a=b,则a±m=b±m。
2.等式两边同乘以(或除以)同一个数(除数不能为零),所得结果仍是等式。
即若a=b,则am=bm,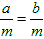 (m≠0)。
(m≠0)。
3.等式具有传递性。
若a1=a2,a2=a3,a3=a4,……an=an,那么a1=a2=a3=a4=……=an
4.等式两边同时乘方(或开方),两边依然相等若a=b 那么有a^c=b^c 或(c次根号a)=(c次根号b)
5.等式的对称性(若a=b,则b=a)。
等式的性质是解方程的基础,很多解方程的方法都要运用到等式的性质。如移项,运用了等式的性质1;去分母,运用了等式的性质2。
运用等式的性质,涉及除法时,要注意转换后,除数不能为0,否则无意义。
含有等号的式子叫做等式(数学术语)。
形式:把相等的两个数(或字母表示的数)用“=”连接起来。
等式可分为矛盾等式和条件等式。矛盾等式就是左右两边不相等的"等式"。也就是不成立的等式,比如5+2=8,实际上5+2=7,所以5+2=8是一个矛盾等式.有些式子无法判断是不是矛盾等式,比如x-9=2,只有x=11时这个等式才成立(这样的等式叫做条件等式),x≠11时,这个等式就是矛盾等式。
等式的性质:
1.等式两边同加上(或减去)同一个数或同一个整式,所得结果仍是等式。
即若a=b,则a±m=b±m。
2.等式两边同乘以(或除以)同一个数(除数不能为零),所得结果仍是等式。
即若a=b,则am=bm,
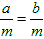 (m≠0)。
(m≠0)。 3.等式具有传递性。
若a1=a2,a2=a3,a3=a4,……an=an,那么a1=a2=a3=a4=……=an
4.等式两边同时乘方(或开方),两边依然相等若a=b 那么有a^c=b^c 或(c次根号a)=(c次根号b)
5.等式的对称性(若a=b,则b=a)。
等式的性质是解方程的基础,很多解方程的方法都要运用到等式的性质。如移项,运用了等式的性质1;去分母,运用了等式的性质2。
运用等式的性质,涉及除法时,要注意转换后,除数不能为0,否则无意义。
拓展
1:等式两边同时被一个数或式子减,结果仍相等。
如果a=b,那么c-a=c-b
2:等式两边取相反数,结果仍相等。
如果a=b,那么-a=-b
3:等式两边不等于0时,被同一个数或式子除,结果仍相等。
如果a=b≠0,那么c/a=c/b
4:等式两边不等于0时,两边取倒数,结果仍相等。
如果a=b≠0,那么1/a=1/b
发现相似题
与“若a、b互为相反数,则在①a+b=0,②|a|=|b|,③a2=b2,④a3=b3,⑤...”考查相似的试题有:
- 下列说法正确的是[ ]A.0是最小的有理数B.0的相反数还是0C.0的倒数是0D.0除以任何数得0
- |-|的相反数是[ ]A.B.-C.3D.-3
- -3的相反数是______.
- 下列说法:①有理数中,0的意义仅表示没有;②整数包括正整数和负整数;③正数和负数统称有理数;④0是最小的整数;⑤负分数是有理...
- 下列各组数中,互为相反数的是A.2与B.与1C.与D.与
- a与b互为相反数,且都不等于0,n为正整数,则下列各组中一定互为相反数的是( )A.an与bnB.a2n与b2nC.a2n+1与b2n+1D.a2n-...
- -2的倒数是( )A..B..C.2 .D.-2.
- 有这样四句话:(1)﹣4是相反数;(2)﹣4和4都是相反数;(3)﹣4是4的相反数,同样4也是﹣4的相反数;(4)﹣4与4互为相反...
- 5的相反数是( ),-的倒数是( ),-3的绝对值是( )。
- 方程中未知数的系数化成1的依据是( )。