本试题 “(本小题满分14分)本题(1)、(2)、(3)三个选答题,每小题7分,任选2题作答,满分14分,如果多做,则按所做的前两题计分。作答时,先用2B铅笔在答题卡上...” 主要考查您对曲线的参数方程
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 曲线的参数方程
曲线的参数方程的定义:
一般地,在平面直角坐标系中,如果曲线C上任意一点的坐标x、y都是某个变数t的函数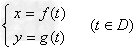 ①,并且对于t的每一个允许值,由方程组①所确定的点P(x,y)都在这条曲线C上,那么方程组①就叫做这条曲线的参数方程。变数t叫做参变量或参变数,简称参数。
①,并且对于t的每一个允许值,由方程组①所确定的点P(x,y)都在这条曲线C上,那么方程组①就叫做这条曲线的参数方程。变数t叫做参变量或参变数,简称参数。
曲线的参数方程的理解与认识:
(1)参数方程的形式:横、纵坐标x、y都是变量t的函数,给出一个t能唯一的求出对应的x、y的值,因而得出唯一的对应点;但横、纵坐标x、y之间的关系并不一定是函数关系。
(2)参数的取值范围:在表述曲线的参数方程时,必须指明参数的取值范围;取值范围的不同,所表示的曲线也可能会有所不同。
(3)参数方程与普通方程的统一性:普通方程是相对参数方程而言的,普通方程反映了坐标变量x与y之间的直接联系,而参数方程是通过变数反映坐标变量x与y之间的间接联系;普通方程和参数方程是同一曲线的两种不同表达形式;参数方程可以与普通方程进行互化。
发现相似题
与“(本小题满分14分)本题(1)、(2)、(3)三个选答题,每小...”考查相似的试题有:
- 己知关于x的方程(m+3)x2-4mx+2m-1=0的两根异号,且负根的绝对值比正根大,那么实数m的取值范围是 A.-3<m<0B.m<-3...
- 在极坐标系中,点 到圆 的圆心的距离为( )A.2B.C.D.
- (本小题满分7分)选修4-4;坐标系与参数方程已知直线经过点M(1,3),且倾斜角为,圆C的参数方程为(是参数),直线与圆C交...
- (本小题满分14分)在直角坐标系中,以为极点,轴的正半轴为极轴建立极坐标系.己知圆的圆心的极坐标为半径为,直线的参数方程...
- (本小题满分8分)直线过点,且倾斜角为.(I)求直线的参数方程;(II)若直线和直线交于点,求.
- 参数方程(为参数)化为普通方程为( )A.y=x-2B.y=x+2C.y=x-2()D.y=x+2()
- 已知曲线C的极坐标方程为,则曲线C上的点到直线为参数)的距离的最大值为 .
- (本题满分12分)已知一动圆与圆外切,同时与圆内切.(1)求动圆圆心的轨迹方程,并说明它是什么样的曲线;(2)直线与M的轨...
- 长为3的线段两端点A,B分别在x轴正半轴和y轴的正半轴上滑动,,点P的轨迹为曲线C.(1)以直线AB的倾斜角为参数,求曲线C的参...
- 在极坐标系中,曲线上有3个不同的点到曲线的距离等于2,则.