本试题 “选修4-4：坐标系与参数方程在直角坐标系xoy中，圆C的参数方程为x=-22+rcosθy=-22+rsinθ(θ为参数r＞0)以O为极点，x轴的非负半轴为极轴，并取相同的长度单位建...” 主要考查您对简单曲线的极坐标方程
圆的参数方程
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 简单曲线的极坐标方程
- 圆的参数方程
曲线的极坐标方程的定义：
一般地，在极坐标系中，如果平面曲线C上任意一点的极坐标中至少有一个满足方程f（ρ，θ）=0，并且坐标适合方程f（ρ，θ）=0的点都在曲线上，那么方程f（ρ，θ）=0叫做曲线C的极坐标方程。
求曲线的极坐标方程的常用方法：
直译法、待定系数法、相关点法等。
圆心为（α，β）（a＞0），半径为a的圆的极坐标方程为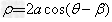
，此圆过极点O。
直线的极坐标方程：
直线的极坐标方程是ρ=1/（2cosθ＋4sinθ）。
圆的极坐标方程：
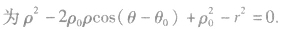
这是圆在极坐标系下的一般方程。
过极点且半径为r的圆方程：
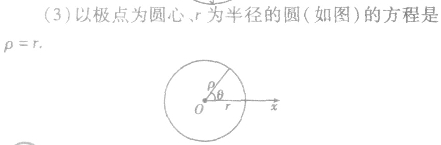
圆的参数方程：
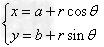（θ∈[0，2π）），（a，b）为圆心坐标，r为圆的半径，θ为参数（x，y）为经过点的坐标。
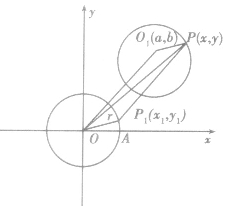
圆心为原点，半径为r的圆的参数方程：
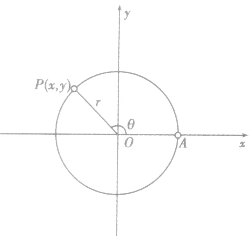
如图，如果点P的坐标为(x，y)，圆半径为r，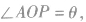
根据三角函数定义，点P的横坐标x、纵坐标y都是θ的函数，即
发现相似题
与“选修4-4：坐标系与参数方程在直角坐标系xoy中，圆C的参数方程...”考查相似的试题有：
- 在极坐标系中，圆ρ=2cosθ的圆心到直线ρsin(θ-π4)=22的距离为______．
- 已知极坐标系的极点在直角坐标系的原点O处，极轴与x轴的正半轴重合．直线l的参数方程为x=1+12ty=32t（t为参数），圆C的极坐标...
- 已知直线的参数方程为为参数)，以坐标原点为极点，轴的正半轴为极轴建立极坐标系，圆的极坐标方程为．求：（1）求圆的直角坐...
- （坐标系与参数方程选做题）已知曲线C的极坐标方程是ρ=6sinθ，以极点为坐标原点，极轴为x的正半轴，建立平面直角坐标系，直线...
- 在极坐标系中，已知曲线设与交于点（I）求点的极坐标；（II）若动直线过点，且与曲线交于两个不同的点求的最小值.
- 已知椭圆的极坐标方程是ρ=，那么它的短轴长是（ ） A． B． C． D．
- 已知直线l的极坐标方程为ρsin(θ+π4)=22，圆M的参数方程为x=-2+2cosθy=-1+2sinθ（θ为参数），则圆M上的点到直线l的最短距离为_...
- 已知抛物线的极坐标方程为ρ=41-cosθ，则此抛物线的准线极坐标方程为______．
- 选修4-4：坐标系与参数方程在直角坐标平面内，以坐标原点O为极点，沿x轴的正半轴为极轴建立极坐标系．曲线C的极坐标方程是ρ=4...
- 在极坐标系中，过点且平行于极轴的直线的极坐标方程是 A． B． C． D．