本试题 “我会判断。(对的打“√”,错的打“×”)1.比的前项和后项同时乘上或同时除以相同的数,比值不变。[ ]2.一根1米长的绳子剪去和剪去米后,剩下的长度相等。[ ]3...” 主要考查您对分数的认识及意义
轴对称,轴对称图形
倒数
比的认识
圆的定义(认识)和圆周率
圆的周长
圆的面积
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 分数的认识及意义
- 轴对称,轴对称图形
- 倒数
- 比的认识
- 圆的定义(认识)和圆周率
- 圆的周长
- 圆的面积
分数的认识:
1、单位“1”

2、分数
把单位“1”平均分成若干份,表示这样一份或者几份的数叫做分数。
如:

一堆糖,平均分成2份,每份是这堆糖的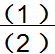
一堆糖,平均分成3份,2份是这堆糖的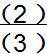
一堆糖,平均分成4份,3份是这堆糖的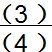
一堆糖,平均分成6份,5份是这堆糖的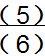
3、分数单位:表示其中一份的数就是分数单位。如 的分数单位是
的分数单位是
分数的意义:
把一个物体或一个计量单位平均分成若干份,这样的一份或几份可用分数表示。在分数里,中间的横线叫做分数线;分数线下面的数叫做分母,表示把单位“1”平均分成多少份;分数线上面的数叫做分子,表示有这样的多少份。
1、单位“1”

2、分数
把单位“1”平均分成若干份,表示这样一份或者几份的数叫做分数。
如:

一堆糖,平均分成2份,每份是这堆糖的
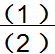
一堆糖,平均分成3份,2份是这堆糖的
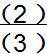
一堆糖,平均分成4份,3份是这堆糖的
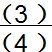
一堆糖,平均分成6份,5份是这堆糖的
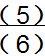
3、分数单位:表示其中一份的数就是分数单位。如
 的分数单位是
的分数单位是
分数的意义:
把一个物体或一个计量单位平均分成若干份,这样的一份或几份可用分数表示。在分数里,中间的横线叫做分数线;分数线下面的数叫做分母,表示把单位“1”平均分成多少份;分数线上面的数叫做分子,表示有这样的多少份。
如果一个图形沿着一条直线对折,直线两边的图形能够完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴。
学过的图形中,线段、角、等腰三角形、等边三角形、长方形、正方形、等腰梯形、圆形、扇形都是轴对称图形,各自有不同数目的对称轴。
学过的图形中,线段、角、等腰三角形、等边三角形、长方形、正方形、等腰梯形、圆形、扇形都是轴对称图形,各自有不同数目的对称轴。
倒数定义:
乘积是1的两个数叫做互为倒数。
求法:
1.求一个分数的倒数,例如3/4,我们只须把3/4这个分数的分子和分母交换位置,即得3/4的倒数为4/3。
2.求一个整数的倒数,只须把这个整数看成是分母为1的分数,然后再按求分数倒数的方法即可得到。
如12,即12/1,再把12/1这个分数的分子和分母交换位置,把分子做分母,分母做分子,则有1/12。 即12倒数是1/12。
说明:倒数是本身的数是1和-1。(0没有倒数)
倒数的特点:一个正实数(1除外)加上它的倒数一定大于2。
比的概念:
两个数相除又叫做两个数的比。这里的两个数,可以是同类量,也可以是不同类量。
例如:长方形的长是6,宽是4,长和宽的比是6比4,宽和长的比是4比6。
组成比例的四个数,叫做比例的项,两端的两项叫做比例的外项,中间的两项叫做比例的内项。
比是由一个前项和一个后项组成的除法算式,只不过把“÷”改成了“:”(比号)而已,但除法算式表示的是一种运算,而比则表示两个数的关系。和分数的分数线类似。
比的写法:
比如6÷4用比的形式写作6:4。“︰”是比号,读作“比”。
比号前面的数叫做比的前项,比号后面的数叫做比的后项(比的后项不能为0)。而本例中6是这个比的前项,4是这个比的后项。
比值:
用比的前项除以比的后项得到一个数,这个数就是比值。比值可以用分数表示,也可以用小数或整数表示。
例如:1:3的比值=1÷3=1/3;1/3也是一种写法,作比时读作一比三,做分数时读作三分之一。
两个比值相等的比可以组成比例,用“=”号连接。
例如:50:25=6:3
圆的定义:
其一:平面上到定点的距离等于定长的点的集合叫圆。
其二:平面上一条线段,绕它的一端旋转360°,留下的轨迹叫圆。
圆周率:
等于圆的周长与直径的比,是个常量,用“π”表示。
圆的特点:
圆就是平面上一种曲线图形。
圆上任意一点到圆心的距离都相等,这个距离就是圆的半径,用字母r表示。
圆上两点之间的部分叫做弧。
通过圆心并且两端都在圆上的线段叫做圆的直径。用字母d表示。
在一个圆里,有无数条半径,无数条直径,直径的长是半径的2倍。
在同一个圆内,所有的半径都相等,直径也都相等。
圆是轴对称图形,它的对称轴是直径,圆有无数条对称轴。
圆的周长计算公式:
圆的周长=直径×圆周率=2×半径×圆周率;C=πd=2πr。(r—半径,d—直径,π—圆周率)
圆的周长=直径×圆周率=2×半径×圆周率;C=πd=2πr。(r—半径,d—直径,π—圆周率)
圆的面积公式:
圆的面积=半径×半径×圆周率;
S=π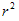 (r—半径,d—直径,π—圆周率)
(r—半径,d—直径,π—圆周率)
圆环面积:
外圆面积-内圆面积;
S=π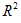 -π
-π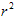 =π(
=π(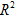 -
-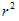 )(R—外圆半径,r—内圆半径)
)(R—外圆半径,r—内圆半径)
圆的面积=半径×半径×圆周率;
S=π
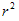 (r—半径,d—直径,π—圆周率)
(r—半径,d—直径,π—圆周率)圆环面积:
外圆面积-内圆面积;
S=π
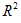 -π
-π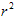 =π(
=π(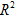 -
-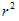 )(R—外圆半径,r—内圆半径)
)(R—外圆半径,r—内圆半径) 发现相似题
与“我会判断。(对的打“√”,错的打“×”)1.比的前项和后项同时乘...”考查相似的试题有:
- 男生人数占全班人数的34,把______看作单位“1”.
- 一张正方形的纸平均分成了8份,每份是这张纸的( )。
- 在○里填上“>”“
- 无限小数3.9595…是______小数,循环节是______,保留整数是______,精确到十分位是______.
- 1的倒数比2的倒数大.______.
- 要画一个周长是12.56厘米的圆,则圆规两脚之间的距离应是( )厘米.A.4B.2C.无法确定
- 小圆的直径是大圆直径的34,小圆周长是大圆周长的______,小圆面积是大圆面积的______.
- 推导圆面积的计算公式,通常采用______法,使拼成的圆形近似于______,它的长相当于圆的______,宽相当于圆的______,所以圆...
- 从一个边长是10分米的正方形纸里剪一个最大的圆,这个圆的周长是______分米,面积是______平方分米.
- 如果大圆直径是小圆直径的3倍,那么大圆面积是小圆面积的( )倍. A.3 B.6 C.9 D.12