本试题 “宇航员站在某一星球距离表面h高度处,以初速度v0沿水平方向抛出一个小球,经过时间t后小球落到星球表面,已知该星球的半径为R,引力常量为G,求:(1)该星球...” 主要考查您对平抛运动
计算天体质量与密度
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 平抛运动
- 计算天体质量与密度
平抛运动的定义:
将物体以一定的初速度沿水平方向抛出,不考虑空气阻力,物体只在重力作用下所做的运动,叫做平抛运动。
平抛运动的特性:
以抛出点为坐标原点,水平初速度V0,竖直向下的方向为y轴正方向,建立如图所示的坐标系,在该坐标系下,对任一时刻t: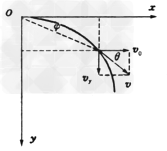
①位移
分位移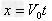 (水平方向),
(水平方向),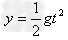 (竖直方向);
(竖直方向);
合位移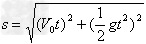 ,
, (φ为合位移与x轴夹角)。
(φ为合位移与x轴夹角)。
②速度
分速度 (水平方向),Vy=gt(竖直方向);
(水平方向),Vy=gt(竖直方向);
合速度 ,
,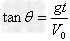 (θ为合速度V与x轴夹角)。
(θ为合速度V与x轴夹角)。
③平抛运动时间: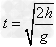 (取决于竖直下落的高度)。
(取决于竖直下落的高度)。
④水平射程: (取决于竖直下落的高度和初速度)。
(取决于竖直下落的高度和初速度)。
类平抛运动:
(1)定义当物体所受的合外力恒定且与初速度垂直时,物体做类平抛运动。
(2)类平抛运动的分解方法
①常规分解法:将类平抛运动分解为沿初速度方向的匀速直线运动和垂直于初速度方向(即沿合力的方向)的匀加速直线运动,两分运动彼此独立,互不影响,且与合运动具有等时性。
②特殊分解法:对于有些问题,可以过抛出点建立适当的直角坐标系,将加速度分解为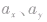 ,,初速度
,,初速度 分解为
分解为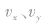 ,然后分别在x、y方向上列方程求解。
,然后分别在x、y方向上列方程求解。
(3)类平抛运动问题的求解思路
根据物体受力特点和运动特点判断该问题属于类平抛运动问题——求出物体运动的加速度——根据具体问题选择用常规分解法还是特殊分解法求解。
(4)类抛体运动
当物体在巨力作用下运动时,若物体的初速度不为零且与外力不在一条直线上,物体所做的运动就是类抛体运动。
在类抛体运动中可采用正交分解法处理问题,基本思路为:
①建立直角坐标系,将外力、初速度沿这两个方向分解。
②求出这两个方向上的加速度、初速度。
③确定这两个方向上的分运动性质,选择合适的方程求解。
计算天体质量与密度:
1、用万有引力定律求天体的质量:通过观天体卫星运动的周期T和轨道半径r或天体表面的重力加速度g和天体的半径R,就可以求出天体的质量M。
2、用万有引力定律计算天体的平均密度:通过观测天体表面运动卫星的周期T,就可以求出天体的密度ρ。
计算天体质量与密度:
1、用万有引力定律求天体的质量:通过观天体卫星运动的周期T和轨道半径r或天体表面的重力加速度g和天体的半径R,就可以求出天体的质量M。以地球的质量的计算为例
①若已知月球绕地球做匀速圆周运动的周期T和半径r,根据: 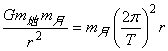 ,得:
,得:![]() ;
;
②若已知月球绕地球做匀速圆周运动的线速度v和半径r,根据: ![]() ,得:
,得:![]() ;
;
③若已知月球绕地球做匀速圆周运动的线速度v和周期T,根据: ![]() 和
和![]() ,得:
,得:![]() ;
;
④若已知地球的半径R和地球表面的重力加速度g,根据: ![]() ,得:
,得:![]() ——此式通常被称为黄金代换式。
——此式通常被称为黄金代换式。
2、用万有引力定律计算天体的平均密度:通过观测天体表面运动卫星的周期T,就可以求出天体的密度ρ。
天体球体积:V=![]() ;天体密度:
;天体密度:![]() (由
(由![]() ,
,![]() ,
,![]() ,r指球体半径,R指轨道半径,当R=r时,
,r指球体半径,R指轨道半径,当R=r时,![]() )。
)。
知识点拨:
科学真是迷人.地球、太阳等天体的质量是多少?天平无法测量.但在我们学习了万有引力定律之后,我们便可以通过它来"称量".求天体质量和密度方法:在地面附近万有引力近似等于物体的重力.由于地球的自转,因而地球表面上的物体随地球自转时需要向心力.所以重力实际上只是万有引力的一个分力,另一个分力就是物体随地球自转时需要的向心力,这个分力与万有引力相比很小忽略不计,可近似认为万有引力等于物体的重力。
与“宇航员站在某一星球距离表面h高度处,以初速度v0沿水平方向抛...”考查相似的试题有:
- 长度L=0.4m的细线,拴着一个质量m=0.4kg的小球,在竖直平面内作圆周运动,小球运动到最低点时离地面高度h=0.8m,此时细线受到...
- 如图所示,在同一位置,以10 m/s水平抛出的物体飞行时间tl后落在斜面上,以20 m/s水平抛出的物体飞行时间t2后落在斜面上,则...
- 如图所示,水平地面上有一个坑,其竖直截面为半圆。ab为沿水平方向的直径。若在a点以初速度v0沿ab方向抛出一小球,小球会击中...
- 在研究平抛物体运动的实验中,用一张印有小方格的纸记录轨迹,小方格的边长=1.25cm。若小球在平抛运动途中的几个位置如图中a...
- 如图所示,一网球运动员将球在边界处正上方水平向右击出,球刚好过网落在图中位置(不计空气阻力),相关数据如图,下列说法...
- 如图所示,一个人用一根长1m,只能承受46N拉力的绳子,拴着一个质量为1kg的小球,在竖直平面内做圆周运动.已知圆心O离地面h=...
- 横截面为直角三角形的两个相同斜面如图紧靠在一起,固定在水平面上,它们的倾角都是30°.小球从左边斜面的顶点以不同的初速度...
- 如图所示,在水平地面上固定一个倾角θ=37°、表面光滑的斜面体,物体A以v1=6m/s的初速度沿斜面上滑,同时在物体A的正上方,有...
- 下列关于平抛运动的说法中正确的是( )A.平抛运动是变加速运动B.任意两段相等时间内速度变化不相同C.任意两段时间内加速...
- 宇航员在地球表面以一定初速度竖直上抛一小球,经过时间t小球落回原处;若他在某星球表面以相同的初速度竖直上抛同一小球,需...