本试题 “连续投掷一枚质量均匀的硬币,10次中出现正面的次数记为x.(1)求随机变量x的数学期望E(x);(2)求10次投掷中出现正面次数多于出现背面次数的概率P(x>5...” 主要考查您对古典概型的定义及计算
离散型随机变量的期望与方差
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 古典概型的定义及计算
- 离散型随机变量的期望与方差
基本事件的定义:
一次试验连同其中可能出现的每一个结果称为一个基本事件。
等可能基本事件:
若在一次试验中,每个基本事件发生的可能性都相同,则称这些基本事件为等可能基本事件。
古典概型:
如果一个随机试验满足:(1)试验中所有可能出现的基本事件只有有限个;
(2)每个基本事件的发生都是等可能的;
那么,我们称这个随机试验的概率模型为古典概型.
古典概型的概率:
如果一次试验的等可能事件有n个,那么,每个等可能基本事件发生的概率都是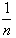 ;如果某个事件A包含了其中m个等可能基本事件,那么事件A发生的概率为
;如果某个事件A包含了其中m个等可能基本事件,那么事件A发生的概率为 。
。
古典概型解题步骤:
(1)阅读题目,搜集信息;
(2)判断是否是等可能事件,并用字母表示事件;
(3)求出基本事件总数n和事件A所包含的结果数m;
(4)用公式 求出概率并下结论。
求出概率并下结论。
求古典概型的概率的关键:
求古典概型的概率的关键是如何确定基本事件总数及事件A包含的基本事件的个数。
数学期望的定义:
称 为ξ的数学期望或平均数,均值,数学期望又简称为期望,它反映了随机变量取值的平均水平。
为ξ的数学期望或平均数,均值,数学期望又简称为期望,它反映了随机变量取值的平均水平。
方差的定义:
称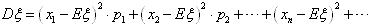 为ξ的均方差,简称为方差,
为ξ的均方差,简称为方差,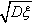 叫做随机变量ξ的标准差,记作:
叫做随机变量ξ的标准差,记作: 。
。
期望与方差的性质:
(1)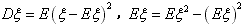 ;
;
(2)若η=aξ+b,则 ;
;
(3)若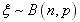 ,则
,则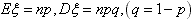 ;
;
(4)若ξ服从几何分布,则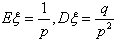 。
。
求均值(数学期望)的一般步骤:
(1)首先判断随机变量是否服从二点分布、二项分布或超几何分布,若服从,则直接用公式求均值.(2)若不服从特殊的分布,则先求出随机变量的分布列,再利用公式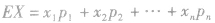 求均值。
求均值。
方差的求法:
(1)若随机变量X服从二点分布或二项分布,则直接利用方差公式可求.
(2)若随机变量X不服从特殊的分布时,求法为:
发现相似题
与“连续投掷一枚质量均匀的硬币,10次中出现正面的次数记为x.(...”考查相似的试题有:
- 设关于x的一元二次方程为x2+2ax+b2=0,(1)设a是0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求上述...
- 从{1,2,3,4,5}中随机选取一个数为a,从{1,2,3}中随机选取一个数为b,则b>a的概率是[ ]A、B、C、D、
- 一堆除颜色外其他特征都相同的红白两种颜色的球若干个,已知红球的个数比白球的多,但比白球的2倍少,若把每一个白球都记作数...
- 袋中有6个球,其中4个白球,2个红球,从袋中任意取出两球,求下列事件的概率:(1)A:取出的两球都是白球;(2)B:取出的两球...
- 甲、乙两人参加一项智力测试.已知在备选的10道题中,甲能答对其中的6道题,乙能答对其中的8道题.规定每位参赛者都从备选题...
- (12分)高三年级班参加高考体检,个班中,任选个班先参加视力检查. (I)求这个班中恰有个班班级序号是偶数的概率;(II)设...
- 某工厂在试验阶段大量生产一种零件.这种零件有A、B两项技术指标需要检测,设各项技术指标达标与否互不影响.若A项技术指标达...
- 如果X是离散型随机变量,Y=3X+2,那么( ) A.E(Y)=3E(X)+2,D(Y)=9D(X)+2 B.E(Y)=3E(X)+2,D(Y)=9D(X) C...
- (本小题满分13分)设S是不等式x2-x-60的解集,整数m,nS。(Ⅰ)记“使得m+n=0成立的有序数组(m,n)”为事件A,试列举A包含的基...
- 为了参加师大附中第23届田径运动会的开幕式,高三年级某6个班联合到集市购买了6根竹竿,作为班旗的旗杆之用,它们的长度分别...