本试题 “跳水是一项优美的水上运动,图甲是2008年北京奥运会跳水比赛中小将陈若琳和王鑫在跳台上腾空而起的英姿。其中陈若琳的体重约为30kg,身高约为1.40m,她站在离...” 主要考查您对竖直上抛运动
从运动情况确定受力
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 竖直上抛运动
- 从运动情况确定受力
竖直上抛运动:
将物体以一定初速度沿竖直方向向上抛出,物体只在重力作用下运动(不考虑空气阻力作用),叫做竖直上抛运动。
竖直上抛运动的公式:
vt=v0-gt;h=v0t-![]() gt2;速度位移公式:vt2-v02=-2gh。
gt2;速度位移公式:vt2-v02=-2gh。
运动特征:
①运动到最高点v=0,a=-g(取竖直向下方向为正方向);
②能上升的最大高度hmax=![]() ;
;
③质点在通过同一高度位置时,上升速度与下落速度大小相等;物体在通过一段高度过程中,上升时间与下落时间相等,![]() 。
。
④物体只受重力作用,具有竖直向上的初速度。
运动性质:
初速度不为零的匀变速直线运动。
竖直上抛的处理方法:
1、分段处理法:
①上升阶段:已知v0,a=-g,vt=0的匀减速直线运动,取向上为正方向较方便。所以运动规律为
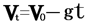 ,
, ,
,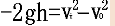
故,上升时间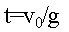 ,最大高度
,最大高度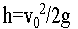 。
。
②最高点v=0,可是不处于静止状态,因为a=g。
③下降阶段:自由落体运动,取向下为正方向较方便。
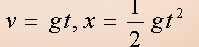
2、对称性:
①竖直上抛的物体上抛达到最大高度与从这一高度落回抛出点所用的时间相等。
②竖直上抛物体在上升和下落过程中经过同一位置时的速度大小相等方向相反。
3、V-t图像:
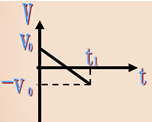
4、整体分析法:
将全过程看成是加速度为-g的匀变速直线运动,应用公式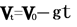 ,
,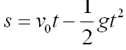
(1)s为正,表示质点在抛出点的上方,s为负表示在抛出点的下方。
(2)由同一s求出的t、可能有两个解,要注意分清其意义。
(3)算出的vt>0表示物体在向上过程中,vt<0表示物体在向下过程中;s>0表示物体在抛出点上方,s<0表示物体在抛出点下方.
从运动情况确定受力:
1、知道物体的运动情况,应用运动学公式求出物体的加速度,再应用牛顿第二定律,推断或者求出物体的受力情况。
2、分析这类问题的关键是抓住受力情况和运动情况的桥梁——加速度。
3、求解动力学这两类问题的思路,可由下面的框图来表示。
瞬时加速度问题的解决方法:
分析物体在某一时刻的瞬时加速度,关键是分析瞬时前后的受力情况及运动状态,再由牛顿第二定律求出瞬时加速度。此类问题应注意以下两种基本模型。
(1)刚性绳(或接触面):可认为是一种不发生明显形变就能产生弹力的物体。若剪断(或脱离)后,其弹力立即消失,不需要考虑形变恢复时间。一般题目中所给的细绳(线)和接触面,在不加特殊说明时,均可按此模型处理。解决此模型的关键在于分析情景突变后的过程,利用过程的初状态分析求解状态突变后的瞬时加速度。
(2)弹簧(或橡皮绳):此类物体的特点是形变量大,形变恢复需要较长时间。在瞬时问题中,其弹力的大小往往可以看成不变。但当弹簧的一端不与有质量的物体连接时,轻弹簧的形变不需要时间,弹力可以突变。解决此类问题时需利用情景突变前的受力来确定情景突变后瞬间的受力及加速度。
动力学范围的整体法与隔离法:
处理连接体问题的方法有整体法和隔离法。
1.整体法将一组连接体作为一个整体看待,牛顿第二定律中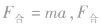 是整体受的合外力,只分析整体所受的外力即可(因为连接体的相互作用力是内力,可不分析),简化了受力分析。在研究连接体时,连接体各部分的运动状态可以相同,也可以不同。当连接体各部分运动状态不同时,整体的合外力等于各部分质量与各部分加速度乘积的矢量和,即F合
是整体受的合外力,只分析整体所受的外力即可(因为连接体的相互作用力是内力,可不分析),简化了受力分析。在研究连接体时,连接体各部分的运动状态可以相同,也可以不同。当连接体各部分运动状态不同时,整体的合外力等于各部分质量与各部分加速度乘积的矢量和,即F合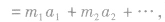 写成分量形式有:
写成分量形式有: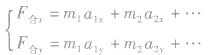
如果待求的问题不涉及系统内部的相互作用时,就可以采用整体法。
2.隔离法在求解连接体的相互作用力时采用,将某个部分从连接体中分离出来,其他部分对它的作用力就成了外力。
整体法与隔离法在研究连接体问题时经常交替使用。
与“跳水是一项优美的水上运动,图甲是2008年北京奥运会跳水比赛...”考查相似的试题有:
- 跳绳是一种健身运动,设某运动员的质量是50 kg ,1 min 跳绳180 次.假定在每次的跳跃中,脚与地面的接触时间为跳跃一次所需...
- 某同学身高1.8m,在运动会上他参加跳高比赛,起跳后身体横着越过了1.8m高度的横杆.据此可估算出他起跳时竖直向上的速度大约...
- 质量不同的甲、乙两小球处于同一高度,甲球以V0初速度做竖直上抛运动、乙球以同样大小的初速度做竖直下抛运动.若m甲>m乙,...
- 如图所示为蹦极运动的示意图.弹性绳的一端固定在O点,另一端和运动员相连.运动员从O点自由下落,至B点弹性绳自然伸直,经过...
- 北京时间2011年2月18日晚6时,在经历了260天的密闭飞行后,中国志愿者王跃走出“火星-500”登陆舱,成功踏上模拟火星表面,在“...
- 质量为1.5t的汽车在前进中受到的阻力是车重的0.05倍,汽车在水平地面上做匀加速直线运动时,5s内速度由36km/h增加到54km/h。...
- 汽车原来以20m/s的速度做匀速直线运动,刹车后做匀减速运动,经4s速度减为0,车的质量为500kg,求刹车过程中所受恒定阻力的大...
- 滑雪运动常在两个斜面和一个平面的组合场地中进行,我们把它简化为理想的情景如图所示,假定运动员和滑板的总质量为m,从O点...
- 如图,在水平地面上有一质量为4.0kg的物块,它与地面的动摩擦因数μ=0.2,在与水平方向夹角为θ=30°的斜向上的拉力F作用下,由...
- 一质量m=2.0 kg的小物块以一定的初速度冲上一倾角为37°足够长的斜面,某同学利用传感器测出了小物块冲上斜面过程中多个时刻的...