本试题 “如图,直线AB,CD相于点O,若∠1=38°,则∠2=( )°,∠3=( )°。” 主要考查您对角的概念
对顶角,同位角,内错角,同旁内角
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 角的概念
- 对顶角,同位角,内错角,同旁内角
角的基本概念:
从静态角度认识角:由一个点出发的两条射线组成的图形叫角;
从动态角度认识角:一条射线绕着它的顶点旋转到另一个位置,则这两条射线组成的图像叫角。有公共端点的两条射线组成的图形叫做角,这个公共端点叫做角的顶点,这两条射线叫做角的边。
①因为射线是向一方无限延伸的,所以角的两边无所谓长短,即角的大小与它的边长无关。
②角的大小可以度量,可以比较。
③根据角的度数,角可以分为锐角、直角、钝角、平角、周角。
角的表示:角可以用大写英文字母、阿拉伯数字或小写的希腊字母表示,如∠1,∠α,∠BAD等。
角的分类:
根据角的度数,角可以分为锐角、直角、钝角、平角、周角。
平角:180。的角,当角的两边在一条直线上时,组成的角叫做平角。即射线OA绕点O旋转,当终边在始边OA的反向延长线上时所成的角;
直角:90。的角,即线OA绕点O旋转,当终边与始边垂直时所成的角,平角的一半叫做直角;
锐角:大于0。小于90。的角,小于直角的角叫做锐角;
钝角:大于90。小于180。的角,大于直角且小于平角的角叫做钝角。
周角:360。的角,即射线OA绕点O旋转,当终边与始边重合时所成的角。
角的性质:
①角的大小与边的长短无关,只与构成角的两条射线的幅度大小有关;
②角的大小可以度量,可以比较;
③角可以参与运算。
角的度量:
角的度量有如下规定:把一个平角180等分,每一份就是1度的角,单位是度,用“。”,1度记作“1°”,n度记作“n°”。把1°的角60等分,每一份叫做1分的角,1分记作“1′”。把1′的角60等分,每一份叫做1秒的角,1秒记作“1″”。1°=60′=3600″。
对顶角:
一个角的两边分别是另一个角的反向延升线,这两个角是对顶角两条直线相交后所得的只有一个公共顶点且两个角的两边互为反向延长线,这样的两个角叫做互为对顶角。
两条直线相交,构成两对对顶角。互为对顶角的两个角相等(对顶角的性质)。
对顶角是针对具有特殊位置的两个角的名称;
对顶角相等反映的是两个角之间的大小关系。
同位角:两个都在截线的同旁,又分别处在被截的两条直线同侧的位置的角叫做同位角。
内错角:两个角分别在截线的两侧,且在两条被截直线之间,具有这样位置关系的一对角叫做内错角。
同旁内角: 两个角都在截线的同一侧,且在两条被截线之间,具有这样位置关系的一对角互为同旁内角。
各种角的关系图示:
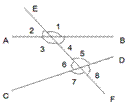
直线AB,CD与EF相交(或者说两条直线AB,CD被第三条直线EF所截),构成八个角。
如图中,∠1与∠3,∠2与∠4是对顶角。
其中∠1与∠5这两个角分别在AB,CD的上方,并且在EF的同侧,像这样位置相同的一对角叫做同位角;
∠3与∠5这两个角都在AB,CD之间,并且在EF的异侧,像这样位置的两个角叫做内错角;
∠3与∠6在直线AB,CD之间,并侧在EF的同侧,像这样位置的两个角叫做同旁内角。
发现相似题
与“如图,直线AB,CD相于点O,若∠1=38°,则∠2=( )°,∠3=( )°。”考查相似的试题有:
- 已知钟表在14点30分时,它的时针和分针构成的角是( )度;比-3°C低6°C的温度是( )度
- 下列说法正确的是[ ]A.平角就是一条直线B.周角就是一条射线C.平角的两条边在同一条直线上D.周角的终边与始边重合,所以周角的...
- 如图,四条表示方向的射线中,表示北偏东60°的是( )A.B.C.D.
- 如图,下列说法中正确的是( ) A.∠BAC和∠DAE不是同一个角 B.∠ABC和∠ACB是同一个角 C.∠ADE可以用∠D表示 D.∠ABC可以用∠B表示
- 有公共顶点的两个角的平分线互相垂直,这两个角是[ ]A.对顶角B.互为补角C.互为邻角D.互为邻补角
- 钟表上2时25分时,时针与分针所成的角是[ ]A.77.5 °B.77 °5′C.75°D.以上答案都不对
- 上午9时30分,时钟的时针和分针所成的角为( )A.90°B.100°C.105°D.120°
- ( )叫做直角,( )叫做锐角,( )叫做钝角.
- 时钟分针长4cm,经过半小时,分针转过的面积是______cm2.
- 下列说法正确的是( )A.同位角相等B.在同一平面内,如果a⊥b,b⊥c,则a⊥cC.相等的角是对顶角D.在同一平面内,如果a∥b,b∥...