二元一次方程组:含有两个未知数,并且所含未知数的项的次数都是1的方程叫做二元一次方程。
把两个含有相同未知数的一次方程联合在一起,那么这两个方程就组成了一个二元一次方程组。
二元一次方程组的解:一般的,二元一次方程组的两个二元一次方程的公共解,叫做二元一次方程组的解。
一般形式为:
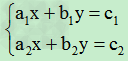
(其中a1,a2,b1,b2不同时为零).
二元一次方程组的特点:1.组成二元一次方程组的两个一次方程不一定都是二元一次方程,但这两个方程必须一共含有两个未知数,如
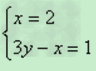
也是二元一次方程组。
2.在方程组的每个方程中,相同字母必须代表同一未知量,否则不能将两个方程合在一起。
3.二元一次方程组中的各个方程应是整式方程。
4.二元一次方程组有时也由两个以上的方程组成。
二元一次方程与二元一次方程组的区别:
|
二元一次方程 |
二元一次方程组 |
| 条件 |
①含有两个未知数;
②含未知数的项的次数都是1;
③整式方程。 |
①含有两个未知数;
②含未知数的项的次数都是1;
③整式方程组(可任意话说你有两个以上的方程) |
| 一般形式 |
ax+by=c(a、b、c都是常数,且a≠0,b≠0) |
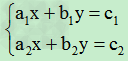
(a1,a2,b1,b2不同时为零). |
| 解的情况 |
无数组解 |
或无数组解或有唯一解或无解 |
| 解的定义 |
适合二元一次方程的每一对未知数的值,叫做这个二元一次方程的一组解 |
二元一次方程组中各个方程的公共解叫做这个二元一次方程组的解 |
二元一次方程组的判定:
①方程组各方程中,相同的字母必须代表同一数量,否则不能将两个方程合在一起.
②怎样检验一组数值是不是某个二元一次方程组的解,常用的方法如下:将这组数值分别代入方程组中的每个方程,只有当这组数值满足其中的所有方程时,才能说这组数值是此方程组的解,否则,如果这组数值不满足其中任一个方程,那么它就不是此方程组的解.