本试题 “如图,半径为1的圆M切直线AB于O点,射线OC从OA 出发绕着O点顺时针方向旋转到OB,旋转过程中OC交⊙M于点P,记∠PMO为x,弓形ONP的面积S=f(x),那么f(x)的大致图...” 主要考查您对函数图象
弧度制、弧度与角度的互化
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 函数图象
- 弧度制、弧度与角度的互化
定义:
点集{(x,y)|y=f(x)}叫做函数y=f(x)的图像。
函数图像的画法:
(1)描点法:
一般我们选择一些特殊点(包括区间端点、最值点、极值点、函数图像与坐标轴的交点等)。
(2)用函数的性质画图
一般我们选择先确定函数的定义域,再看函数是否具有周期性和对称性、奇偶性,这样我们就可以只画出部分图像,之后根据性质直接得到其余部分的图像,然后判断单调性,确定特殊点或渐近线,进而得到函数的大致图像。
(3)通过图像变换画图
(一)平移变化:
Ⅰ水平平移:函数y=f(x+a)的图像可以把函数y=f(x)的图像沿x轴方向向左(a>0)或向右(a<0)平移|a|个单位即可得到;
Ⅱ竖直平移:函数y=f(x+a)的图像可以把函数y=f(x)的图像沿x轴方向向上(a>0)或向下(a<0)平移|a|个单位即可得到.
(二)对称变换:
Ⅰ函数y=f(-x)的图像可以将函数y=f(x)的图像关于y轴对称即可得到;
Ⅱ函数y=-f(x)的图像可以将函数y=f(x)的图像关于x轴对称即可得到;
Ⅲ函数y=-f(-x)的图像可以将函数y=f(x)的图像关于原点对称即可得到;
Ⅳ函数y=f-1(x)的图像可以将函数y=f(x)的图像关于直线y=x对称得到.
函数图像的判断:
这里主要是抽象函数的图像,借助函数的对称性、周期性及单调性确定函数的图像;另外借助导数,就是函数在某点处的切线斜率的变化,体现在函数的图像上就是增长的快还是慢来确定函数的图像。
常用结论:
(1)若函数y=f(x)定义域内任一x的值都满足f(a+x)=f(b-x),则y=f(x)的图像关于直线 成轴对称图形;特别地,y=f(x)满足
成轴对称图形;特别地,y=f(x)满足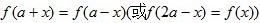 恒成立,则y=f(x)的图像关于直线x=a成轴对称图形;
恒成立,则y=f(x)的图像关于直线x=a成轴对称图形;
(2)函数y=f(x)的图像关于直线x=a及x=b对称,则y=f(x)是周期函数,且2|b-a|是它的一个周期。
1弧度的角的概念:
长度等于半径长的弧所对的圆心角叫做1弧度的角,记作1rad。
弧度制:
用弧度作单位来度量角的制度叫弧度制。
一般地:正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0。
角α的弧度公式:
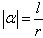 (l表示圆心角α所对的弧长,r表示圆的半径)。
(l表示圆心角α所对的弧长,r表示圆的半径)。
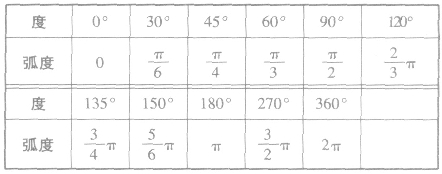
角度与弧度的换算公式:
360°=2π,180°=π,1°=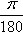 rad≈0.01745rad,1rad=
rad≈0.01745rad,1rad=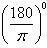 ≈57.30°=57°18′。
≈57.30°=57°18′。
扇形面积公式:
S= lr=
lr= |α|r2。
|α|r2。


与“如图,半径为1的圆M切直线AB于O点,射线OC从OA 出发绕着O点顺...”考查相似的试题有:
- 函数f(x)=axm(1-x)n在区间[0,1]上的图像如图所示,则m,n的值可能为[ ]A.m=1,n=1B.m=1,n=2C.m=2,n=1D.m=3,n=1
- 函数y= (0<a<1)的图象的大致形状是 ( ).
- “龟兔赛跑”讲述了这样的故事:领先的兔子看着慢慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急...
- 下列图象可作为函数y=f(x)的图象的是[ ]A、B、C、D、
- 设函数()满足,,则函数的图像可能是( )
- -120°的弧度数是[ ]A、B、C、D、
- ,则( )A.B.-C.D.-
- 若角的终边落在直线上,则= 。
- 若θ是第二象限角,试判断sin(cosθ)的符号.
- 与-263°角终边相同的角的集合是A.B.C.D.